State-of-the-Art Digest
Graph & Geometric ML in 2024: Where We Are and What’s Next (Part I — Theory & Architectures)
Following the tradition from previous years, we interviewed a cohort of distinguished and prolific academic and industrial experts in an attempt to summarise the highlights of the past year and predict what is in store for 2024. Past 2023 was so ripe with results that we had to break this post into two parts. This is Part I focusing on theory & new architectures, see also Part II on applications.

Image by Authors with some help from DALL-E 3.
The post is written and edited by Michael Galkin and Michael Bronstein with significant contributions from Johannes Brandstetter, İsmail İlkan Ceylan, Francesco Di Giovanni, Ben Finkelshtein, Kexin Huang, Chaitanya Joshi, Chen Lin, Christopher Morris, Mathilde Papillon, Liudmila Prokhorenkova, Bastian Rieck, David Ruhe, Hannes Stärk, and Petar Veličković.
The legend we will be using throughout the text:
? - year’s highlight
?️ - challenges
➡️ - current/next developments
?- predictions/speculations
Theory of Graph Neural Networks
Michael Bronstein (Oxford), Francesco Di Giovanni (Oxford), İsmail İlkan Ceylan (Oxford), Chris Morris (RWTH Aachen)
Message Passing Neural Networks & Graph Transformers
Graph Transformers are a relatively recent trend in graph ML, trying to extend the successes of Transformers from sequences to graphs. As far as traditional expressivity results go, these architectures do not offer any particular advantages. In fact, it is arguable that most of their benefits in terms of expressivity (see e.g. Kreuzer et al.) come from powerful structural encodings rather than the architecture itself and such encodings can in principle be used with MPNNs.
In a recent paper, Cai et al. investigate the connection between MPNNs and (graph) Transformers showing that an MPNN with a virtual node — an auxiliary node that is connected to all other nodes in a specific way — can simulate a (graph) Transformer. This architecture is non-uniform, i.e., the size and structure of the neural networks may depend on the size of the input graphs. Interestingly, once we restrict our attention to linear Transformers (e.g., Performer) then there is a uniform result: there exists a single MPNN using a virtual node that can approximate a linear transformer such as Performer on any input of any size.
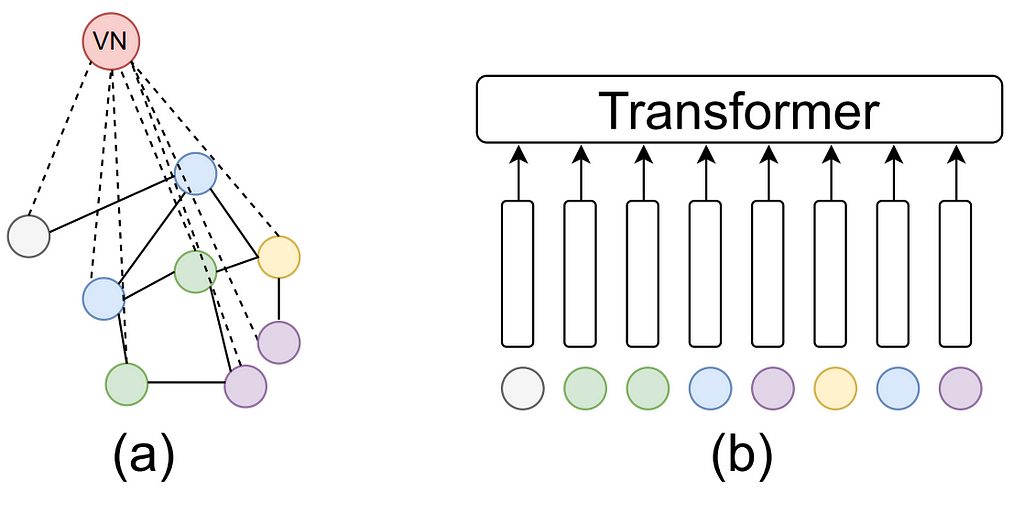
Figure from Cai et al.: (a) MPNN with a virtual node, (b) a Transformer.
This is related to the discussions on whether graph transformer architectures present advantages for capturing long-range dependencies when compared to MPNNs. Graph transformers are compared to MPNNs that include a global computation component through the use of virtual nodes, which is a common practice. Cai et al. empirically show that MPNNs with virtual nodes can surpass the performance of graph transformers on the Long-Range Graph Benchmark (LRGB, Dwivedi et al.) Moreover, Tönshoff et al. re-evaluate MPNN baselines on the LRGB benchmark to find out that the earlier reported performance gap in favor of graph transformers was overestimated due to suboptimal hyperparameter choices, essentially closing the gap between MPNNs and graph Transformers.
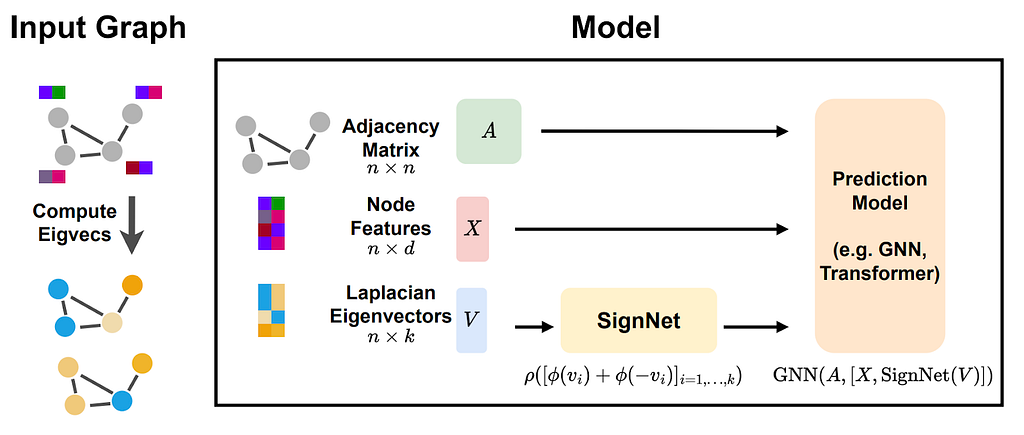
Figure from Lim et al.: SignNet pipeline.
It is also well-known that common Laplacian positional encodings (e.g., LapPE), are not invariant to the changes of signs and basis of eigenvectors. The lack of invariance makes it easier to obtain (non-uniform) universality results, but these models do not compute graph invariants as a consequence. This has motivated a body of work this year, including the study of sign and basis invariant networks (Lim et al., 2023a) and sign equivariant networks (Lim et al., 2023b). These findings suggest that more research is necessary to theoretically ground the claims commonly found in the literature regarding the comparisons of MPNNs and graph transformers.
Graph components, biconnectivity, and planarity
Figure originally by Zyqqh at Wikipedia.
Zhang et al. (2023a) brings the study of graph biconnectivity to the attention of graph ML community. There are many results presented by Zhang et al. (2023a) relative to different biconnectivity metrics. It has been shown that standard MPNNs cannot detect graph biconnectivity unlike many existing higher-order models (i.e., those that can match the power of 2-FWL). On the other hand, Graphormers with certain distance encodings and subgraph GNNs such as ESAN can detect graph biconnectivity.
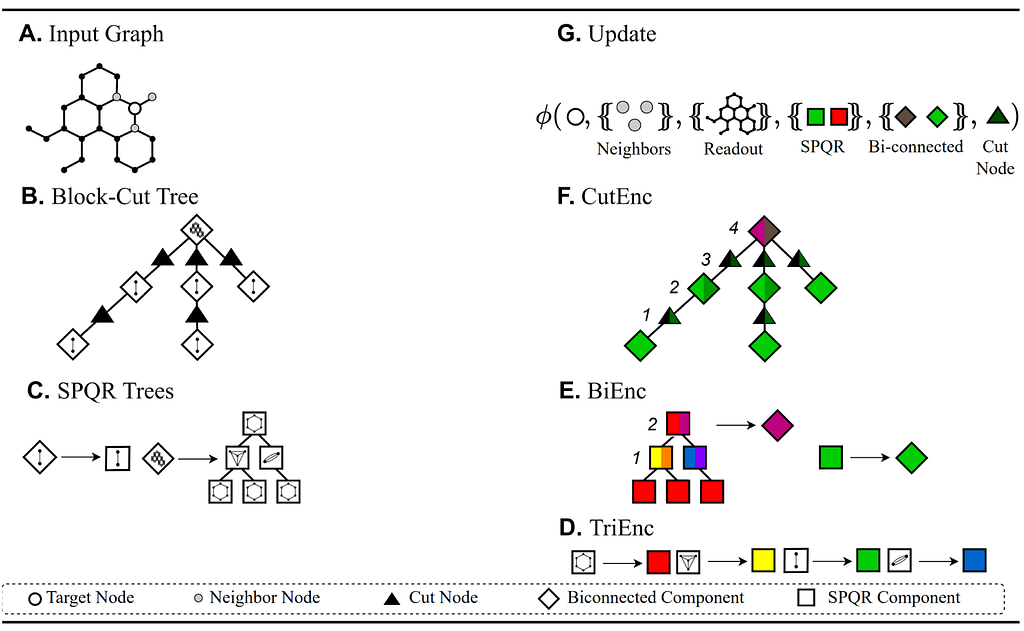
Figure from Dimitrov et al. (2023): LHS shows the graph decompositions (A-C) and RHS shows the associated encoders (D-F) and the update equation (G).
Dimitrov et al. (2023) rely on graph decompositions to develop dedicated architectures for learning with planar graphs. The idea is to align with a variation of the classical Hopcroft & Tarjan algorithm for planar isomorphism testing. Dimitrov et al. (2023) first decompose the graph into its biconnected and triconnected components, and afterwards learn representations for nodes, cut nodes, biconnected components, and triconnected components. This is achieved using the classical structures of Block-Cut Trees and SPQR Trees which can be computed in linear time. The resulting framework is called PlanE and contains architectures such as BasePlanE. BasePlanE computes isomorphism-complete graph invariants and hence it can distinguish any pair of planar graphs. The key contribution of this work is to design architectures for efficiently learning complete invariants of planar graphs while remaining practically scalable. It is worth noting that 3-FWL is known to be complete on planar graphs (Kiefer et al., 2019), but this algorithm is not scalable.
Aggregation functions: A uniform expressiveness study
It was broadly argued that different aggregation functions have their place, but this had not been rigorously proven. In fact, in the non-uniform setup, sum aggregation with MLPs yields an injective mapping and as a result subsumes other aggregation functions (Xu et al., 2020), which builds on earlier results (Zaheer et al., 2017). The situation is different in the uniform setup, where one fixed model is required to work on all graphs. Rosenbluth et al. (2023) show that sum aggregation does not always subsume other aggregations in the uniform setup. If, for example, we consider an unbounded feature domain, sum aggregation networks cannot even approximate mean aggregation networks. Interestingly, even for the positive results, where sum aggregation is shown to approximate other aggregations, the presented constructions generally require a large number of layers (growing with the inverse of the approximation error).
Convergence and zero-one laws of GNNs on random graphs
GNNs can in principle be applied to graphs of any size following training. This makes an asymptotic analysis in the size of the input graphs very appealing. Previous studies of the asymptotic behaviour of GNNs have focused on convergence to theoretical limit networks (Keriven et al., 2020) and their stability under the perturbation of large graphs (Levie et al., 2021).
In a recent study, Adam-Day et al. (2023) proved a zero-one law for binary GNN classifiers. The question being tackled is the following: How do binary GNN classifiers behave as we draw Erdos-Rényi graphs of increasing size with random node features? The main finding is that the probability that such graphs are mapped to a particular output by a class of GNN classifiers tends to either zero or to one. That is, the model eventually maps either all graphs to zero or all graphs to one. This result applies to GCNs as well as to GNNs with sum and mean aggregation.
The principal import of this result is that it establishes a novel uniform upper bound on the expressive power of GNNs: any property of graphs which can be uniformly expressed by these GNN architectures must obey a zero-one law. An example of a simple property which does not asymptotically tend to zero or one is that of having an even number of nodes.
The descriptive complexity of GNNs
Grohe (2023) recently analysed the descriptive complexity of GNNs in terms of Boolean circuit complexity. The specific circuit complexity class of interest is TC0. This class contains all languages which are decided by Boolean circuits with constant depth and polynomial size, using only AND, OR, NOT, and threshold (or, majority) gates. Grohe (2023) proves that the graph functions that can be computed by a class of polynomial-size bounded-depth family of GNNs lie in the circuit complexity class TC0. Furthermore, if the class of GNNs are allowed to use random node initialization and global readout as in Abboud el al. (2020) then there is a matching lower bound in that they can compute exactly the same functions that can be expressed in TC0. This establishes an upper bound on the power of GNNs with random node features, by requiring the class of models to be of bounded depth (fixed #layers) and of size polynomial. While this result is still non-uniform, it improves the result of Abboud el al. (2020) where the construction can be worst-case exponential.
A fine-grained expressivity study of GNNs
Numerous recent works have analyzed the expressive power of MPNNs, primarily utilizing combinatorial techniques such as the 1-WL for the graph isomorphism problem. However, the graph isomorphism objective is inherently binary, not giving insights into the degree of similarity between two given graphs. Böker et al. (2023) resolve this issue by deriving continuous extensions of both 1-WL and MPNNs to graphons. Concretely, they show that the continuous variant of 1-WL delivers an accurate topological characterization of the expressive power of MPNNs on graphons, revealing which graphs these networks can distinguish and the difficulty level in separating them. They provide a theoretical framework for graph and graphon similarity, combining various topological variants of classical characterizations of the 1-WL. In particular, they characterize the expressive power of MPNNs in terms of the tree distance, which is a graph distance based on the concept of fractional isomorphisms, and substructure counts via tree homomorphisms, showing that these concepts have the same expressive power as the 1-WL and MPNNs on graphons. Interestingly, they also validated their theoretical findings by showing that randomly initialized MPNNs, without training, show competitive performance compared to their trained counterparts.
Expressiveness results for Subgraph GNNs
Subgraph-based GNNs were already a big trend in 2022 (Bevilacqua et al., 2022, Qian et al., 2022). This year, Zhang et al. (2023b) established more fine-grained expressivity results for such architectures. The paper investigates subgraph GNNs via the so-called Subgraph Weisfeiler-Leman Tests (SWL). Through this, they show a complete hierarchy of SWL with strictly growing expressivity. Concretely, they define equivalence classes for SWL-type algorithms and show that almost all existing subgraph GNNs fall in one of them. Moreover, the so-called SSWL achieves the maximal expressive power. Interestingly, they also relate SWL to several existing expressive GNNs architectures. For example, they show that SWL has the same expressivity as the local versions of 2-WL (Morris et al., 2020). In addition to theory, they also show that SWL-type architectures achieve good empirical results.
Expressive power of architectures for link prediction on KGs
The expressive power of architectures such as RGCN and CompGCN for link prediction on knowledge graphs has been studied by Barceló et al. (2022). This year, Huang et al. (2023) generalized these results to characterize the expressive power of various other model architectures.
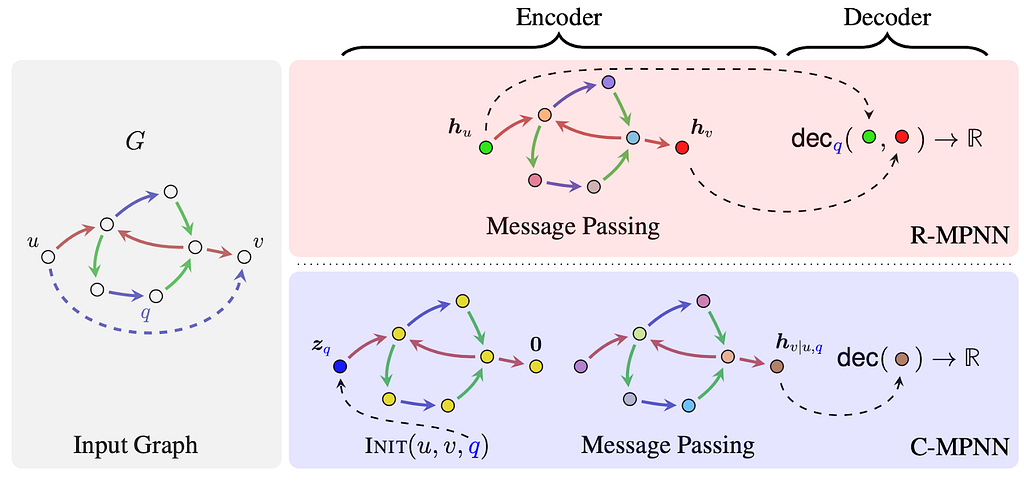
Figure from Huang et al. (2023): The figure compares the respective mode of operations in R-MPNNs and C-MPNNs.
Huang et al. (2023) introduced the framework of conditional message passing networks (C-MPNNs) which includes architectures such as NBFNets. Classical relational message passing networks (R-MPNNs) are unary encoders (i.e., encoding graph nodes) and rely on a binary decoder for the task of link prediction (Zhang, 2021). On the other hand, C-MPNNs serve as binary encoders (i.e., encoding pairs of graph nodes) and as a result, are more suitable for the binary task of link prediction. C-MPNNs are shown to align with a relational Weisfeiler-Leman algorithm that can be seen as a local approximation of 2WL. These findings explain the superior performance of NBFNets and alike over, e.g., RGCNs. Huang et al. (2023) also present uniform expressiveness results in terms of precise logical characterizations for the class of binary functions captured by C-MPNNs.
Over-squashing and expressivity
Over-squashing is a phenomenon originally described by Alon & Yahav in 2021 as the compression of exponentially-growing receptive fields into fixed-size vectors. Subsequent research (Topping et al., 2022, Di Giovanni et al., 2023, Black et al., 2023, Nguyen et al., 2023) has characterised over-squashing through sensitivity analysis, proving that the dependence of the output features on hidden representations from earlier layers, is impaired by topological properties such as negative curvature or large commute time. Since the graph topology plays a crucial role in the formation of bottlenecks, graph rewiring, a paradigm shift elevating the graph connectivity to design factor in GNNs, has been proposed as a key strategy for alleviating over-squashing (if you are interested, see the Section on Exotic Message Passing below).
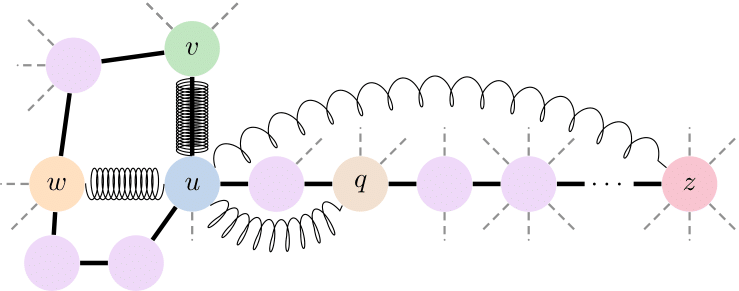
For the given graph, the MPNN learns stronger mixing (tight springs) for nodes (v, u) and (u, w) since their commute time is small, while nodes (u, q) and (u, z), with high commute-time, have weak mixing (loose springs). Source: Di Giovanni et al., 2023
Over-squashing is an obstruction to the expressive power, for it causes GNNs to falter in tasks with long-range interactions. To formally study this, Di Giovanni et al., 2023 introduce a new metric of expressivity, referred to as “mixing”, which encodes the joint and nonlinear dependence of a graph function on pairs of nodes’ features: for a GNN to approximate a function with large mixing, a necessary condition is allowing “strong” message exchange between the relevant nodes. Hence, they postulate to measure over-squashing through the mixing of a GNN prediction, and prove that the depth required by a GNN to induce enough mixing, as required by the task, grows with the commute time — typically much worse than the shortest-path distance. The results show how over-squashing hinders the expressivity of GNNs with “practical” size, and validate that it arises from the misalignment between the task (requiring strong mixing between nodes i and j) and the topology (inducing large commute time between i and j).
The “mixing” of a function pertains to the exchange of information between nodes, whatever this information is, and not to its capacity to separate node representations. In fact, these results also hold for GNNs more powerful than the 1-WL test. The analysis in Di Giovanni et al., (2023) offers an alternative approach for studying the expressivity of GNNs, which easily extends to equivariant GNNs in 3D space and their ability to model interactions between nodes.
Generalization and extrapolation capabilities of GNNs
The expressive power of MPNNs has achieved a lot of attention in recent years through its connection to the WL test. While this connection has led to significant advances in understanding and enhancing MPNNs’ expressive power (Morris et al, 2023a), it does not provide insights into their generalization performance, i.e., their ability to make meaningful predictions beyond the training set. Surprisingly, only a few notable contributions study MPNNs’ generalization behaviors, e.g., Garg et al. (2020), Kriege et al. (2018), Liao et al. (2021), Maskey et al. (2022), Scarselli et al. (2018). However, these approaches express MPNNs’ generalization ability using only classical graph parameters, e.g., maximum degree, number of vertices, or edges, which cannot fully capture the complex structure of real-world graphs. Further, most approaches study generalization in the non-uniform regime, i.e., assuming that the MPNNs operate on graphs of a pre-specified order.
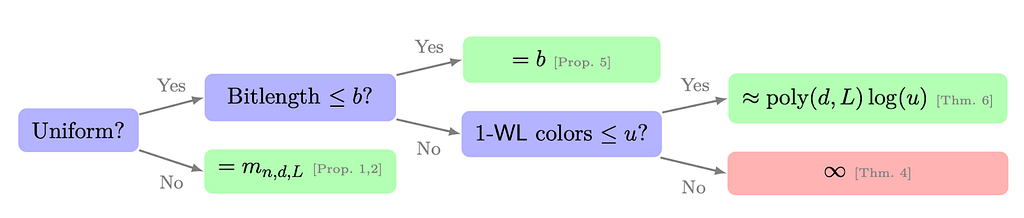
Figure from Morris et al. (2023b): Overview of the generalization capabilities of MPNNs and their link to the 1-WL.
Hence, Morris et al. (2023b) showed a tight connection between the expressive power of the 1-WL and generalization performance. They investigate the influence of graph structure and the parameters’ encoding lengths on MPNNs’ generalization by tightly connecting 1-WL’s expressivity and MPNNs’ Vapnik–Chervonenkis (VC) dimension. To that, they show several results.
1️⃣ First, in the non-uniform regime, they show that MPNNs’ VC dimension depends tightly on the number of equivalence classes computed by the 1-WL over a set of graphs. In addition, their results easily extend to the k-WL and many recent expressive MPNN extensions.
2️⃣ In the uniform regime, i.e., when graphs can have arbitrary order, they show that MPNNs’ VC dimension is lower and upper bounded by the largest bitlength of its weights. In both the uniform and non-uniform regimes, MPNNs’ VC dimension depends logarithmically on the number of colors computed by the 1-WL and polynomially on the number of parameters. Moreover, they also empirically show that their theoretical findings hold in practice to some extent.
? Predictions time!
Christopher Morris (RWTH Aachen)
➡️ For example, we need to understand how graph structure and various architectural parameters influence generalization. Moreover, the dynamics of SGD for training GNNs are currently understudied and not well understood, and more works will study this.
İsmail İlkan Ceylan (Oxford)
➡️ In this case, we can identify a better connection to generalization, because if a property cannot be expressed uniformly then the model cannot generalise to larger graph sizes.
➡️ This year, we may also see expressiveness studies that target graph regression or graph generation, which remain under-explored. There are good reasons to hope for learning algorithms which are isomorphism-complete on larger graph classes, strictly generalizing the results for planar graphs.
➡️ It is also time to develop a theory for learning with fully relational data (i.e., knowledge hypergraphs), which will unlock applications in relational databases!
Francesco Di Giovanni (Oxford)
In terms of future theoretical developments of GNNs, I can see two directions that deserve attention.
➡️ Second, I believe it would be valuable to develop alternative paradigms of expressivity, which more directly focus on approximation power (of graph functions and their derivatives) and identify precisely the tasks which are hard to learn. The latter direction could also be particularly meaningful for characterising the power of equivariant GNNs in 3D space, where measurements of expressivity might need to be decoupled from the 2D case in order to be better aligned with tasks coming from the scientific domain.
At the end: a fun fact about where WL went in 2023

Portraits: Ihor Gorsky
Predictions from the 2023 post
(1) More efforts on creating time- and memory-efficient subgraph GNNs.
❌ not really
(2) Better understanding of generalization of GNNs
✅ yes, see the subsections on oversquashing and generalization
(3) Weisfeiler and Leman visit 10 new places!
❌ (4 so far) Grammatical, indifferent, measurement modeling, paths
New and exotic message passing
Ben Finkelshtein (Oxford), Francesco Di Giovanni (Oxford), Petar Veličković (Google DeepMind)
Petar Veličković (Google DeepMind)
Over the years, it has become part of common folklore that the development of message passing operators has saturated. What I find particularly exciting about the progress made in 2023 is that, from several independent research groups (including our own), a unified novel direction has emerged: let’s start considering the impact of time in the GNN ⏳.
? Time has already been leveraged in GNN design when it is explicitly provided in the input (in spatiotemporal or fully dynamic graphs). This year, it has started to feature in research of GNN operators on static graph inputs. Several works are dropping the assumption of a unified, synchronised clock ⏱️ which forces all messages in a layer to be sent and received at once.
1️⃣ The first such work, GwAC ?, only played with rudimentary randomised message scheduling, but provided proofs for why such processing might yield significant improvements in expressive power. Co-GNNs ? carry the torch further, demonstrating a more elaborate and fine-tuned message scheduling mechanism which is node-centric, allowing each node to choose when to send ? or receive ? messages. Co-GNNs also provide a practical method for training such schedulers by gradient descent. While the development of such asynchronous GNN models is highly desirable, we must also acknowledge the associated scalability issues — our present frontier hardware is not designed to efficiently scale such sequential systems.
2️⃣ In our own work on asynchronous algorithmic alignment, we instead opt to design a synchronous GNN, but constrain its message, aggregation, and update functions such that the GNN would yield identical embeddings even if parts of its dataflow were made asynchronous. This led us to an exciting journey through monoids, 1-cocycles, and category theory, resulting in a scalable GNN model that achieves superior performance on many CLRS-30 tasks.

A possible execution trace of an asynchronous GNN. While traditional GNNs send and receive all messages synchronously, under our framework, at any step the GNN may choose to execute any number of possible operations (depicted here with a collection on the right side of the graph). Source: Dudzik et al.
➡️ Lastly, it is worth noting that for certain special choices of message scheduling, we do not need to make modifications to synchronous GNNs’ architecture — and may instead resort to dynamic graph rewiring. DREW and Half-Hop are two concurrently published papers at ICML’23 which embody the principle of using graph rewiring to slow down message passing ?. In DREW, a message from each node is actually sent to every other node, but it takes k layers before a message will reach a neighbour that is k hops away! Half-Hop, on the other hand, takes a more lenient approach, and just randomly decides whether or not to introduce a “slow node” which extends the path between any two nodes connected by an edge. Both approaches naturally alleviate the oversmoothing problem, as messages travelling longer distances will oversmooth less.
Whether it is used for message passing design, GNN dataflow or graph rewiring, in 2023 we have just started to grasp the importance of time — even when time variation is not explicitly present in our dataset.
Ben Finkelshtein (Oxford)
The time-dependent message passing paradigm presented in Co-GNNs is a learnable generalisation of message passing, which allows each node to decide how to propagate information from or to its neighbours, thus enabling a more flexible flow of information. The nodes are regarded as players that can either broadcast to neighbors that listen and listen to neighbors that broadcast (like in classical message-passing), Broadcast to neighbors that listen, or Isolate (neither listen nor broadcast).
The interplay between these actions and the ability to change them locally and dynamically allows CoGNNs to determine a task-specific computational graph (which can be considered as a form of dynamic and directed rewiring, learn different action distribution for two nodes with different node features (both feature- and structure-based). CoGNNs allow asynchronous updates across nodes and also yield unique node identifiers with high probability, which allows them to distinguish any pair of graphs (more expressive than 1-WL, at the expense of equivariance holding only in expectation).
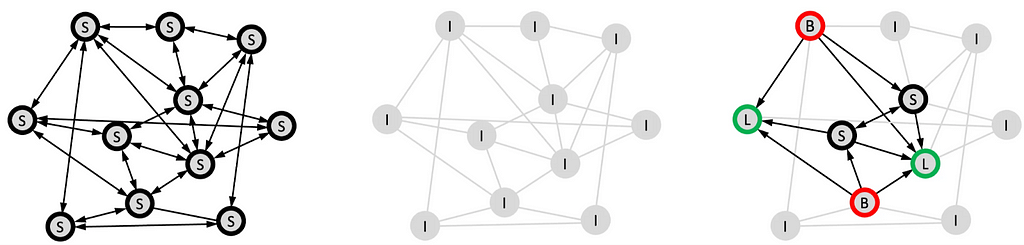
Left to right: classical MPNNs (all nodes broadcast & listen), DeepSets (all nodes isolate), and generic CoGNNs. Figure from blog post.
Check the Medium post for more details:
Co-operative Graph Neural Networks
Francesco Di Giovanni (Oxford)
️? Graph rewiring broadly entails altering the connectivity of the input graph to facilitate the solution of the downstream task. Recently, this has often targeted bottlenecks in the graph, thereby adding (and removing) edges to improve the flow of information. While the emphasis has been on where messages are exchanged, recent works (discussed above) have shed light on the relevance of when messages should be exchanged as well. One rationale behind these approaches, albeit often implicit, is that the hidden representations built by the layers of a GNN, provide the graph with an (artificially) dynamic component, even though the graph and input features are static. This perspective can be leveraged in several ways.
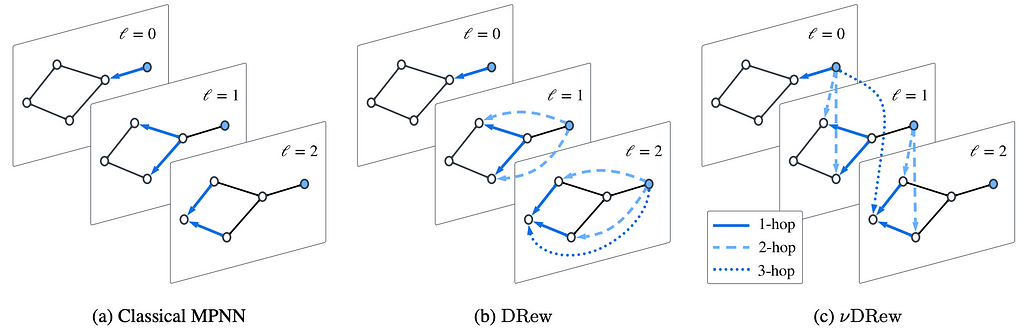
In the classicical MPNN setting, at every layer information only travels from a node to its immediate neighbours. In DRew, the graph changes based on the layer, with newly added edges connecting nodes at distance r from layer r − 1 onward. Finally, in νDRew, we also introduce a delay mechanism equivalent to skip-connections between different nodes based on their mutual distance. Source: Gutteridge et al.
➡️ One framework that has particularly embraced such an angle is DRew, which extends any message-passing model in two ways: (i) it connects nodes at distance r directly, but only from layer r onwards; (ii) when nodes are connected, a delay is applied to their message exchange, based on their mutual distance. As the figure above illustrates, (i) allows the network to better retain the inductive bias, as nodes that are closer, interact earlier; (ii) instead acts as distance-aware skip connections, thereby facilitating the propagation of gradients for the loss. Most likely, it is for this reason, and not prevention of over-smoothing (which hardly has an impact for graph-level tasks), that the framework significantly enhances the performance of standard GNNs at larger depths (more details can be found in this blog post).
? Predictions: I believe that the deep implications of extending message-passing over the “time” component would start to emerge in the coming year. Works like DRew have only scratched the surface of why rewiring over time (beyond space) might benefit the training of GNNs, drastically affecting their accuracy response across different depth regimes.
➡️ More broadly, I hope that theoretical and practical developments of graph rewiring could be translated into scientific domains, where equivariant GNNs are often applied to 3D problems which either do not have a natural graph structure (making the question of “where” messages should be exchanged ever more relevant) or (and) exhibit natural temporal (multi-scale) properties (making the question of “when” messages should be exchanged likely to be key for reducing memory constraints and retaining the right inductive bias).
Geometry, Topology, Geometric Algebras & PDEs
Johannes Brandstetter (JKU Linz), Michael Galkin (Intel), Mathilde Papillon (UC Santa Barbara), Bastian Rieck (Helmholtz & TUM), and David Ruhe (U Amsterdam)
2023 brought the most comprehensive introduction to (and a survey of) Geometric GNNs covering the most basic and necessary concepts with a handful of examples: A Hitchhiker’s Guide to Geometric GNNs for 3D Atomic Systems (Duval, Mathis, Joshi, Schmidt, et al.). If you ever wanted to learn from scratch the core architectures powering recent breakthroughs of graph ML in protein design, material discovery, molecular simulations, and more — this is what you need!
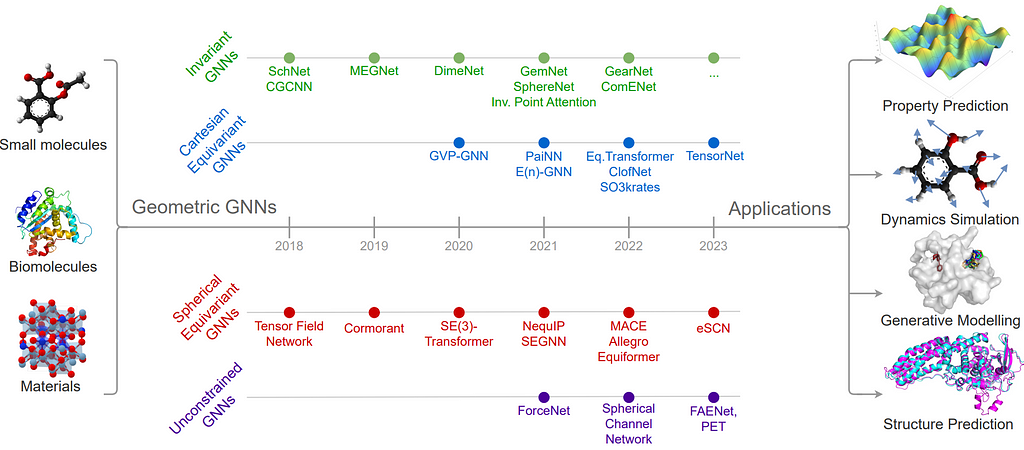
Timeline of key Geometric GNNs for 3D atomic systems, characterised by the type of intermediate representations within layers. Source: Duval, Mathis, Joshi, Schmidt, et al.
Topology
? Working with topological structures in 2023 has become much easier for both researchers and practitioners thanks to the amazing efforts of the PyT team and their suite of resources: TopoNetX, TopoModelX, and TopoEmbedX. TopoNetX is pretty much the networkx for topological data. TopoNetX supports standard structures like cellular complexes, simplicial complexes, and combinatorial complexes. TopoModelX is a PyG-like library for deep learning on topological data and implements famous models like MPSN and CIN with a neat unified interface (the original PyG implementations are quite tangled). TopoEmbedX helps to train embedding models on topological data and supports core algorithms like Cell2Vec.
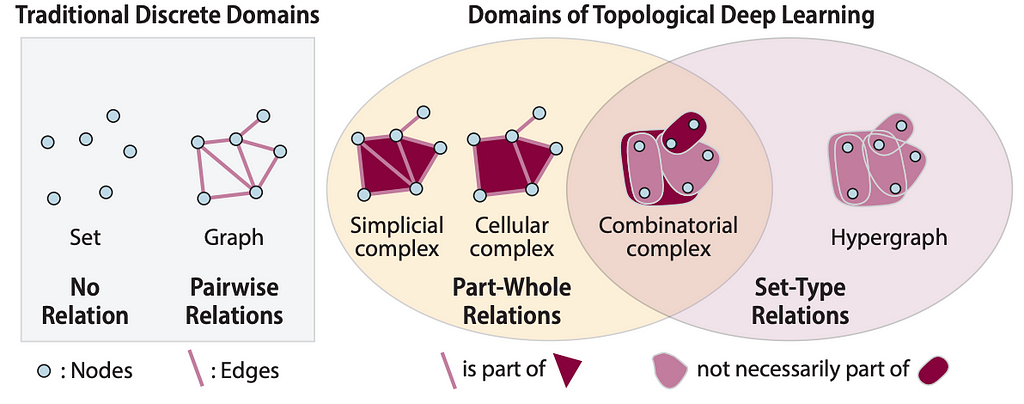
Domains: Nodes in blue, (hyper)edges in pink, and faces in dark red. Source: TopoNetX, Papillon et al
? A great headstart to the field and basic building blocks of those topological networks are the papers by Hajij et al and by Papillon et al. A notable chunk of models was implemented by the members of the Topology, Algebra, and Geometry in Data Science (TAG) community that regularly organizes topological workshops at ML conferences.
Mathilde Papillon (UCSB)
➡️ Message-passing models were only built upon and benchmarked against other models of the same domain, e.g., the simplicial complex community remained insular to the hypergraph community. To make matters worse, most models adopted a unique mathematical notation. Deciding which model would be best suited to a given application seemed like a monumental task. A unification theory proposed by Hajij et al offered a general scheme under which all models could be systematically described and classified. We applied this theory to the literature to produce a comprehensive yet concise survey of message passing in topological deep learning that also serves as an accessible introduction to the field. We additionally provide a dictionary listing all the model architectures in one unifying notation.
➡️ To further unify the field, we organized the first Topological Deep Learning Challenge, hosted at the 2023 ICML TAG workshop and recorded via this white paper by Papillon et al. The goal was to foster reproducible research by crowdsourcing the open-source implementation of neural networks on topological domains. As part of the challenge, participants from around the world contributed implementations of pre-existing topological deep learning models in TopoModelX. Each submission was rigorously unit-tested and included benchmark training on datasets loaded from TopoNetX. It is our hope that this one-stop-shop suite of consistently implemented models will help practitioners test-drive topological methods for new applications and developments in 2024.
Bastian Rieck (Helmholtz & TUM)
2023 was an exciting year for topology-driven machine learning methods. On the one hand, we saw more integrations with geometrical concepts like curvature, thus demonstrating the versatility of hybrid geometrical-topological models. For instance, in ‘Curvature Filtrations for Graph Generative Model Evaluation,’ we showed how to employ curvature as a way to select suitable graph generative models. Here, curvature serves as a ‘lens’ that we use to extract graph structure information, while we employ persistent homology, a topological method, to compare this information in a consistent fashion.

An overview of the pipeline for evaluating graph generative models using discrete curvature. The ordering on edges gives rise to a curvature filtration, followed by a corresponding persistence diagram and landscape. For graph generative models, we select a curvature, apply this framework element-wise, and evaluate the similarity of the generated and reference distributions by comparing their average landscapes. Source: Southern, Wayland, Bronstein, and Rieck.
➡️ Another direction that serves to underscore that topology-driven methods are becoming a staple in graph learning research uses topology to assess the expressivity of graph neural network models. Sometimes, as in a very fascinating work from NeurIPS 2023 by Immonen et al. this even leads to novel models that leverage both geometrical and topological aspects of graphs in tandem! My own research also aims to contribute to this facet by specifically analyzing the expressivity of persistent homology in graph learning.
➡️ With my great collaborators, we started looking at some alternatives very recently and came up with the concept of neural differential forms. Differential forms permit us to elegantly build a bridge between geometry and topology by means of the de Rham cohomology — a way to link the integration of certain objects (differential forms), i.e. a fundamentally geometric operation, to topological characteristics of input data. With some additional constructions, the de Rham cohomology permits us to learn geometric descriptions of graphs (or higher-order combinatorial complexes) and solve learning tasks without having to rely on message passing. The upshot are models with fewer parameters that are potentially more effective at solving such tasks. There’s more to come here, since we have just started scratching the surface!
?My hopeful predictions for 2024 are that we will:
1️⃣ see many more diverse tools from algebraic and differential topology applied to graphs and combinatorial complexes,
2️⃣ better understand message passing on higher-order input data, and
3️⃣ finally obtain better parallel algorithms for persistent homology to truly unleash its power in a deep learning setting. A recent paper on spectral sequences by Torras-Casas reports some very exciting results that show the great prospects of this technique.
Geometric Algebras
Johannes Brandstetter (JKU Linz) and David Ruhe (U Amsterdam)
➡️ First, Ruhe et al. applied the quintessence of modern (plane-based) geometric algebra by introducing Geometric Clifford Algebra Networks (GCAN), neural network templates that model symmetry transformations described by various geometric algebras. We saw an intriguing application thereof by Pepe et al. in CGAPoseNet, building a geometry-aware pipeline for camera pose regression. Next, Ruhe et al. introduced Clifford Group Equivariant Neural Networks (CGENN), building steerable O - and E
- and E -equivariant (graph) neural networks of any dimension via the Clifford group. Pepe et al. apply CGENNs to a Protein Structure Prediction (PSP) pipeline, increasing prediction accuracies by up to 2.1%.
-equivariant (graph) neural networks of any dimension via the Clifford group. Pepe et al. apply CGENNs to a Protein Structure Prediction (PSP) pipeline, increasing prediction accuracies by up to 2.1%.
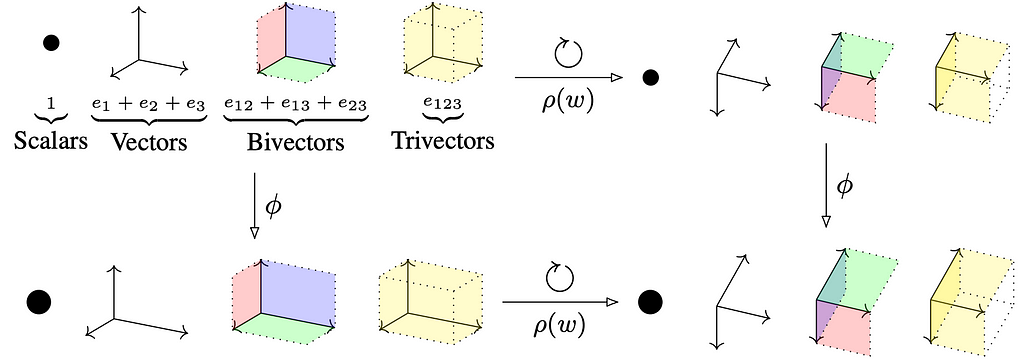
CGENNs (represented with ϕ) are able to operate on multivectors (elements of the Clifford algebra) in an O - or E
- or E -equivariant way. Specifically, when an action ρ(w) of the Clifford group, representing an orthogonal transformation such as a rotation, is applied to the data, the model’s representations corotate. Multivectors can be decomposed into scalar, vector, bivector, trivector, and even higher-order components. These elements can represent geometric quantities such as (oriented) areas or volumes. The action ρ(w) is designed to respect these structures when acting on them. Source: Ruhe et al.
-equivariant way. Specifically, when an action ρ(w) of the Clifford group, representing an orthogonal transformation such as a rotation, is applied to the data, the model’s representations corotate. Multivectors can be decomposed into scalar, vector, bivector, trivector, and even higher-order components. These elements can represent geometric quantities such as (oriented) areas or volumes. The action ρ(w) is designed to respect these structures when acting on them. Source: Ruhe et al.
➡️ Coincidently, Brehmer et al. formulated Geometric Algebra Transformer(GATr), a scalable Transformer architecture that harnesses the benefits of representations provided by the projective geometric algebra and the scalability of Transformers to build E(3)-equivariant architectures. The GATr architecture was extended to other algebras by Haan et al. who also examine which flavor of geometric algebra is best suited for your E(3)-equivariant machine learning problem.
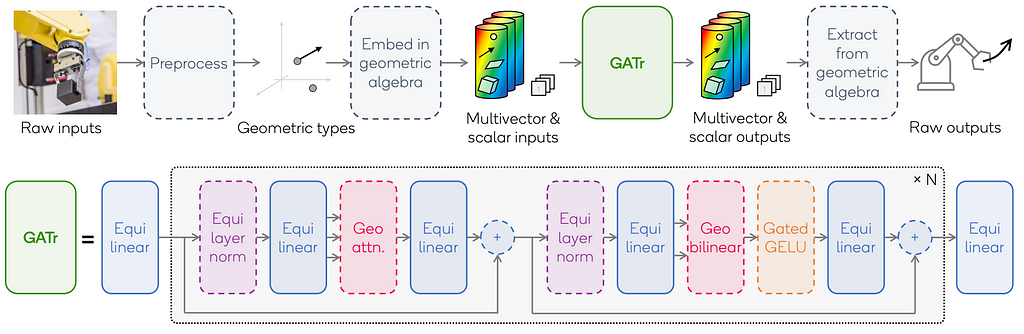
Overview of the GATr architecture. Boxes with solid lines are learnable components, those with dashed lines are fixed. Source: Brehmer et al.
? In 2024, we can expect exciting new applications from these advancements. Some examples include the following.
1️⃣ We can expect explorations of their applicability to molecular data, drug design, neural physics emulations, crystals, etc. Other geometry-aware applications include 3D rendering, pose estimations, and planning for, e.g., robot arms.
2️⃣ We can expect the extension of geometric algebra-based networks to other neural network architectures, such as convolutional neural networks.
3️⃣ Next, the generality of the CGENN allows for explorations in other dimensions, e.g., 2D, but also in settings where data of various dimensionalities should be processed together. Further, they enable non-Euclidean geometries, which have several use cases in relativistic physics.
4️⃣ Finally, GATr and CGENN can be extended and applied to projective, conformal, hyperbolic, or elliptic geometries.
PDEs
Johannes Brandstetter (JKU Linz)
Concerning the landscape of neural PDE modelling, what topics have surfaced or gathered momentum through 2023?
1️⃣ To begin, there is a noticeable trend towards modelling PDEs on and within intricate geometries, necessitating a mesh-based discretization of space. This aligns with the overarching goal to address increasingly realistic real world problems. For example, Li et al. have introduced Geometry-Informed Neural Operator (GINO) for large-scale 3D PDEs.
2️⃣ Secondly, the development of neural network surrogates for Lagrangian-based simulations is becoming increasingly intriguing. The Lagrangian discretization of space uses finite material points which are tracked as fluid parcels through space and time. The most prominent Lagrangian discretization scheme is called smoothed particle hydrodynamics (SPH), which is the numerical baseline in the LagrangeBench benchmark dataset provided by Toshev et al.
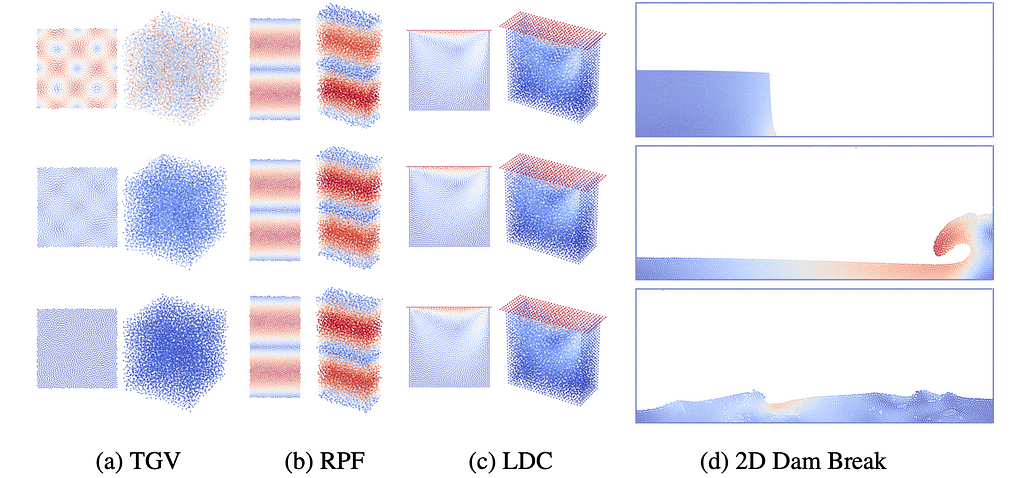
Time snapshots of our datasets, at the initial time (top), 40% (middle), and 95% (bottom) of the trajectory. Color temperature represents velocity magnitude. (a) Taylor Green vortex (2D and 3D), (b) Reverse Poiseuille flow (2D and 3D), © Lid-driven cavity (2D and 3D), (d) Dam break (2D). Source: LagrangeBench by Toshev et al.
3️⃣ Thirdly, diffusion-based modelling is also not stopping for PDEs. We roughly see two directions. The first direction recasts the iterative nature of the diffusion process into a refinement of a candidate state initialised from noise and conditioned on previous timesteps. This iterative refinement was introduced in PDE-Refiner (Lippe et al.) and a variant thereof was already applied in GenCast (Price et al.). The second direction exerts the probabilistic nature of diffusion models to model chaotic phenomena such as 3D turbulence. Examples of this can be found in Turbulent Flow Simulation (Kohl et al.) and in From Zero To Turbulence (Lienen et al.). Especially for 3D turbulence, there are a lot of interesting things that will happen in the near future.
? What to expect in 2024:
1️⃣ More work regarding 3D turbulence modelling.
2️⃣ Multi-modality aspects of PDEs might emerge. This could include combining different PDEs, different resolutions, or different discretization schemes. We are already seeing a glimpse thereof in e.g. Multiple Physics Pretraining for Physical Surrogate Models by McCabe et al.
Predictions from the 2023 post
(1) Neural PDEs and their applications are likely to expand to more physics-related AI4Science subfields; computational fluid dynamics (CFD) will potentially be influenced by GNN.
✅ We are seeing 3D turbulence modelling, geometry-aware neural operators, particle-based neural surrogates, and a huge impact in e.g. weather forecasting.
(2) GNN based surrogates might augment/replace traditional well-tried techniques.
✅ Weather forecasting has become a great success story. Neural network based weather forecasts overtake traditional forecasts (medium range+local forecasts), e.g., GraphCast by Lam et al. and MetNet-3 by Andrychowicz et al.
Robustness and Explainability
Kexin Huang (Stanford)
1️⃣ When discussing the reliability of GNNs, a key criterion is uncertainty quantification — quantifying how much the model knows about the prediction. There are numerous works on estimating and calibrating uncertainty, also designed specifically for GNNs (e.g. GATS). However, they fall short of achieving pre-defined target coverage (i.e. % of points falling into the prediction set) both theoretically and empirically. I want to emphasize that this notion of having a coverage guarantee is critical especially in ML deployment for scientific discovery since practitioners often trust a model with statistical guarantees.
2️⃣ Conformal prediction is an exciting direction in statistics where it has finite sample coverage guarantees and has been applied in many domains such as vision and NLP. But it is unclear if it can be used in graphs theoretically since it is not obvious if the exchangeability assumption holds for graph settings. In 2023, we see conformal prediction has been extended to graphs. Notably, CF-GNN and DAPS have derived theoretical conditions for conformal validity in transductive node-level prediction setting and also developed methods to reduce the prediction set size for efficient downstream usage. More recently, we have also seen conformal prediction extensions to link prediction, non-uniform split, edge exchangeability, and also adaptations for settings where exchangeability does not hold (such as inductive setting).
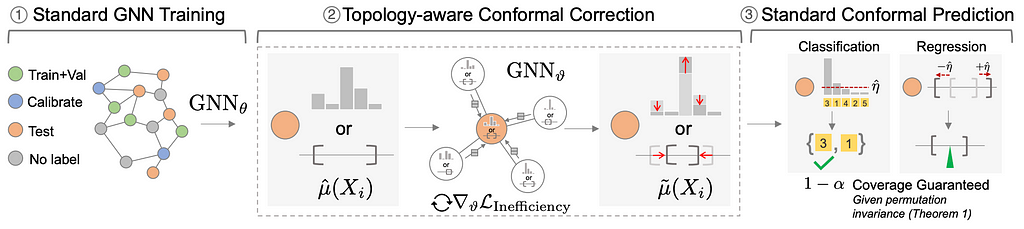
Conformal prediction for graph-structured data. (1) A base GNN model (GNN) that produces prediction scores µ for node i. (2) Conformal correction. Since the training step is not aware of the conformal calibration step, the size/length of prediction sets/intervals (i.e. efficiency) are not optimized. We use a topology-aware correction model that takes µ as the input node feature and aggregates information from its local subgraph to produce an updated prediction µ˜. (3) Conformal prediction. We prove that in a transductive random split setting, graph exchangeability holds given permutation invariance. Thus, standard CP can be used to produce a prediction set/interval based on µ˜ that includes true label with pre-specified coverage rate 1-α. Source: Huang et al.
? Looking ahead, we expect more extensions to cover a wide range of GNN deployment use cases. Overall, I think having statistical guarantees for GNNs is very nice because it enables the trust of practitioners to use GNN predictions.
Graph Transformers
Chen Lin (Oxford)
? In 2023, we have seen the continuation of the rise of Graph Transformers. It has become the common GNN design, e.g., in GATr, the authors attribute its popularity to its “favorable scaling properties, expressiveness, trainability, and versatility”.
1️⃣ Expressiveness of GTs. As mentioned in the GNN Theory section, recent work from Cai et al. (2023) shows the equivalence between MPNNs with a Virtural Node and GTs under a non-uniform setting. This poses a question on how powerful are GTs and what is the source of their representation ability. Zhang et al. (2023) successfully combine a new powerful positional embedding (PE) to improve the expressiveness of their GTs, achieving expressivity over the biconnectivity problem. This gives evidence of the importance of PEs to the expressiveness of GTs. A recent submission GPNN provides a clearer view on the central role of the positional encoding. It has been shown that one can generalize the proof in Zhang et al. (2023) to show how GTs’ expressiveness is decided by various positional encodings.
2️⃣ Positional (Structural) Encoding. Given the importance of PE/SE to GTs, now we turn to the design of those expressive features usually derived from existing graph invariants. In 2022, GraphGPS observed a huge empirical success by combining GTs with various (or even multiple) PE/SEs. In 2023, more powerful PE/SE is available.
Relative Random Walk PE (RRWP) proposed by Ma et al generalizes the random walk structural encoding with the relational part. Together with a new variant of attention mechanism, GRIT achieves a strong empirical performance compared with existing PE/SEs on property prediction benchmarks (SOTA on ZINC). Theoretically, RRWP can approximate the Shortest path distance, personalized PageRank, and heat kernel with a specific choice of parameters. With RRWP, GRIT is more expressive than SPD-WL.
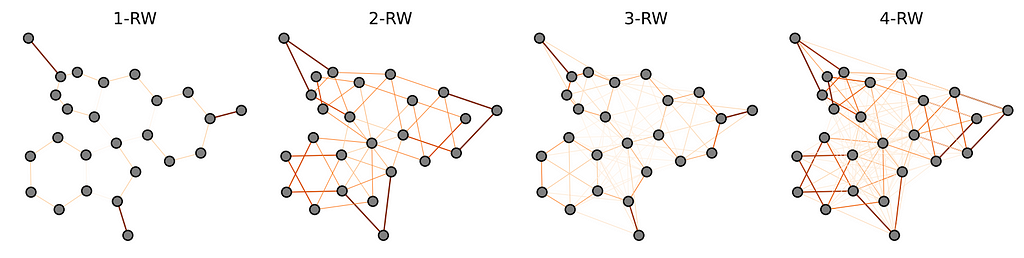
RRWP visualization for the fluorescein molecule, up to the 4th power. Thicker and darker edges indicate higher edge weight. Probabilities for longer random walks reveal higher-order structures (e.g., the cliques evident in 3-RW and the star patterns in 4-RW). Source: Ma et al.
Puny et al proposed a new theoretical framework for expressivity based on Equivariant Polynomials where the expressivity of common GNNs can be improved by having the polynomial features, computed with tensor contractions based on the equivariant basis, as positional encodings. The empirical results are surprising: GatedGCNs is improved from a test MAE of 0.265 to 0.106 with the d-expressive polynomials. It will be very interesting to see if someone combines this with GTs in the future.
3️⃣ Efficient GTs. It remains challenging for GTs to be applied to large graphs due to the O(N²) complexity. In 2023, we saw more works trying to eliminate such difficulty by lowering the computation complexity of GTs. Deac et al used expander graphs for the propagation, which is regularly connected with few edges. Exphormer extended this idea to GT by combining expander graphs with the local neighborhood aggregation and virtual node. Exphormer allows graph transformers to scale to larger graphs (as large as ogbn-arxiv with 169K nodes). It also achieved strong empirical results and ranked top on several Long-Range Graph Benchmark tasks.
? Moving forward to 2024:
Structural biology: Pinder from VantAI, PoseBusters from Oxford, PoseCheck from The Other Place, DockGen, and LargeMix and UltraLarge datasets from Valence Labs
Temporal Graph Benchmark (TGB): Until now, progress in temporal graph learning has been held back by the lack of large high-quality datasets, as well as the lack of proper evaluation thus leading to over-optimistic performance. TGB addresses this by introducing a collection of seven realistic, large-scale and diverse benchmarks for learning on temporal graphs, including both node-wise and link-wise tasks. Inspired by the success of OGB, TGB automates dataset downloading and processing as well as evaluation protocols, and allows users to compare model performance using a leaderboard. Check out the associated blog post for more details.
TpuGraphs from Google Research: the graph property prediction dataset of TPU computational graphs. The dataset provides 25x more graphs than the largest graph property prediction dataset (with comparable graph sizes), and 770x larger graphs on average compared to existing performance prediction datasets on machine learning programs. Google ran Kaggle competition based off TpuGraphs!
LagrangeBench: A Lagrangian Fluid Mechanics Benchmarking Suite — where you can evaluate your favorite GNN-based simulator in a JAX-based environment (for JAX aficionados).
RelBench: Relational Deep Learning Benchmark from Stanford and Kumo.AI: make time-based predictions over relational databases (which you can model as graphs or hypergraphs).
The GNoMe dataset from Google DeepMind: 381k more novel stable materials for your materials discovery and ML potentials models!
Conferences, Courses & Community
The main events in the graph and geometric learning world (apart from big ML conferences) grow larger and more mature: The Learning on Graphs Conference (LoG), Molecular ML (MoML), and the Stanford Graph Learning Workshop. The LoG conference features a cool format with the remote-first conference and dozens of local meetups organized by community members spanning the whole globe from China to UK & Europe to the US West Coast ??? .

The LoG meetups in Amsterdam, Paris, Tromsø, and Shanghai. Source: Slack of the LoG community
Courses, books, and educational resources
Memes of 2023

Commemorating the successes of flow matching in 2023 in the meme and unique t-shirts brought to NeurIPS’23. Right: Hannes Stärk and Michael Galkin are making a statement at NeurIPS’23. Images by Michael Galkin

GNN aggregation functions are actually portals to category theory (Created by Petar Veličković)

Michael Bronstein continues to harass Google by demanding his DeepMind chair at every ML conference, but so far, he has only been offered stools (photo credits: Jelani Nelson and Thomas Kipf).

The authors of this blog post congratulate you upon completing the long read. Michael Galkin and Michael Bronstein with the Meme of 2022 at ICML 2023 in Hawaii (Photo credit: Ben Finkelshtein)
For additional articles about geometric and graph deep learning, see Michael Galkin’s and Michael Bronstein’s Medium posts and follow the two Michaels (Galkin and Bronstein) on Twitter.

Graph & Geometric ML in 2024: Where We Are and What’s Next (Part I — Theory & Architectures) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Graph & Geometric ML in 2024: Where We Are and What’s Next (Part I — Theory & Architectures)
Following the tradition from previous years, we interviewed a cohort of distinguished and prolific academic and industrial experts in an attempt to summarise the highlights of the past year and predict what is in store for 2024. Past 2023 was so ripe with results that we had to break this post into two parts. This is Part I focusing on theory & new architectures, see also Part II on applications.

Image by Authors with some help from DALL-E 3.
The post is written and edited by Michael Galkin and Michael Bronstein with significant contributions from Johannes Brandstetter, İsmail İlkan Ceylan, Francesco Di Giovanni, Ben Finkelshtein, Kexin Huang, Chaitanya Joshi, Chen Lin, Christopher Morris, Mathilde Papillon, Liudmila Prokhorenkova, Bastian Rieck, David Ruhe, Hannes Stärk, and Petar Veličković.
- Theory of Graph Neural Networks
1. Message passing neural networks and Graph Transformers
2. Graph components, biconnectivity & planarity
3. Aggregation functions & uniform expressivity
4. Convergence & zero-one laws of GNNs
5. Descriptive complexity of GNNs
6. Fine-grained expressivity of GNNs
7. Expressivity results for Subgraph GNNs
8. Expressivity for Link Prediction and Knowledge Graphs
9. Over-squashing & Expressivity
10. Generalization and Extrapolation capabilities of GNNs
11. Predictions time! - New and Exotic Message Passing
- Beyond Graphs
1. Topology
2. Geometric Algebras
3. PDEs - Robustness & Explainability
- Graph Transformers
- New Datasets & Benchmarks
- Conferences, Courses & Community
- Memes of 2023
The legend we will be using throughout the text:
? - year’s highlight
?️ - challenges
➡️ - current/next developments
?- predictions/speculations
Theory of Graph Neural Networks
Michael Bronstein (Oxford), Francesco Di Giovanni (Oxford), İsmail İlkan Ceylan (Oxford), Chris Morris (RWTH Aachen)
Message Passing Neural Networks & Graph Transformers
Graph Transformers are a relatively recent trend in graph ML, trying to extend the successes of Transformers from sequences to graphs. As far as traditional expressivity results go, these architectures do not offer any particular advantages. In fact, it is arguable that most of their benefits in terms of expressivity (see e.g. Kreuzer et al.) come from powerful structural encodings rather than the architecture itself and such encodings can in principle be used with MPNNs.
In a recent paper, Cai et al. investigate the connection between MPNNs and (graph) Transformers showing that an MPNN with a virtual node — an auxiliary node that is connected to all other nodes in a specific way — can simulate a (graph) Transformer. This architecture is non-uniform, i.e., the size and structure of the neural networks may depend on the size of the input graphs. Interestingly, once we restrict our attention to linear Transformers (e.g., Performer) then there is a uniform result: there exists a single MPNN using a virtual node that can approximate a linear transformer such as Performer on any input of any size.

Figure from Cai et al.: (a) MPNN with a virtual node, (b) a Transformer.
This is related to the discussions on whether graph transformer architectures present advantages for capturing long-range dependencies when compared to MPNNs. Graph transformers are compared to MPNNs that include a global computation component through the use of virtual nodes, which is a common practice. Cai et al. empirically show that MPNNs with virtual nodes can surpass the performance of graph transformers on the Long-Range Graph Benchmark (LRGB, Dwivedi et al.) Moreover, Tönshoff et al. re-evaluate MPNN baselines on the LRGB benchmark to find out that the earlier reported performance gap in favor of graph transformers was overestimated due to suboptimal hyperparameter choices, essentially closing the gap between MPNNs and graph Transformers.

Figure from Lim et al.: SignNet pipeline.
It is also well-known that common Laplacian positional encodings (e.g., LapPE), are not invariant to the changes of signs and basis of eigenvectors. The lack of invariance makes it easier to obtain (non-uniform) universality results, but these models do not compute graph invariants as a consequence. This has motivated a body of work this year, including the study of sign and basis invariant networks (Lim et al., 2023a) and sign equivariant networks (Lim et al., 2023b). These findings suggest that more research is necessary to theoretically ground the claims commonly found in the literature regarding the comparisons of MPNNs and graph transformers.
Graph components, biconnectivity, and planarity

Figure originally by Zyqqh at Wikipedia.
Zhang et al. (2023a) brings the study of graph biconnectivity to the attention of graph ML community. There are many results presented by Zhang et al. (2023a) relative to different biconnectivity metrics. It has been shown that standard MPNNs cannot detect graph biconnectivity unlike many existing higher-order models (i.e., those that can match the power of 2-FWL). On the other hand, Graphormers with certain distance encodings and subgraph GNNs such as ESAN can detect graph biconnectivity.

Figure from Dimitrov et al. (2023): LHS shows the graph decompositions (A-C) and RHS shows the associated encoders (D-F) and the update equation (G).
Dimitrov et al. (2023) rely on graph decompositions to develop dedicated architectures for learning with planar graphs. The idea is to align with a variation of the classical Hopcroft & Tarjan algorithm for planar isomorphism testing. Dimitrov et al. (2023) first decompose the graph into its biconnected and triconnected components, and afterwards learn representations for nodes, cut nodes, biconnected components, and triconnected components. This is achieved using the classical structures of Block-Cut Trees and SPQR Trees which can be computed in linear time. The resulting framework is called PlanE and contains architectures such as BasePlanE. BasePlanE computes isomorphism-complete graph invariants and hence it can distinguish any pair of planar graphs. The key contribution of this work is to design architectures for efficiently learning complete invariants of planar graphs while remaining practically scalable. It is worth noting that 3-FWL is known to be complete on planar graphs (Kiefer et al., 2019), but this algorithm is not scalable.
Aggregation functions: A uniform expressiveness study
It was broadly argued that different aggregation functions have their place, but this had not been rigorously proven. In fact, in the non-uniform setup, sum aggregation with MLPs yields an injective mapping and as a result subsumes other aggregation functions (Xu et al., 2020), which builds on earlier results (Zaheer et al., 2017). The situation is different in the uniform setup, where one fixed model is required to work on all graphs. Rosenbluth et al. (2023) show that sum aggregation does not always subsume other aggregations in the uniform setup. If, for example, we consider an unbounded feature domain, sum aggregation networks cannot even approximate mean aggregation networks. Interestingly, even for the positive results, where sum aggregation is shown to approximate other aggregations, the presented constructions generally require a large number of layers (growing with the inverse of the approximation error).
Convergence and zero-one laws of GNNs on random graphs
GNNs can in principle be applied to graphs of any size following training. This makes an asymptotic analysis in the size of the input graphs very appealing. Previous studies of the asymptotic behaviour of GNNs have focused on convergence to theoretical limit networks (Keriven et al., 2020) and their stability under the perturbation of large graphs (Levie et al., 2021).
In a recent study, Adam-Day et al. (2023) proved a zero-one law for binary GNN classifiers. The question being tackled is the following: How do binary GNN classifiers behave as we draw Erdos-Rényi graphs of increasing size with random node features? The main finding is that the probability that such graphs are mapped to a particular output by a class of GNN classifiers tends to either zero or to one. That is, the model eventually maps either all graphs to zero or all graphs to one. This result applies to GCNs as well as to GNNs with sum and mean aggregation.
The principal import of this result is that it establishes a novel uniform upper bound on the expressive power of GNNs: any property of graphs which can be uniformly expressed by these GNN architectures must obey a zero-one law. An example of a simple property which does not asymptotically tend to zero or one is that of having an even number of nodes.
The descriptive complexity of GNNs
Grohe (2023) recently analysed the descriptive complexity of GNNs in terms of Boolean circuit complexity. The specific circuit complexity class of interest is TC0. This class contains all languages which are decided by Boolean circuits with constant depth and polynomial size, using only AND, OR, NOT, and threshold (or, majority) gates. Grohe (2023) proves that the graph functions that can be computed by a class of polynomial-size bounded-depth family of GNNs lie in the circuit complexity class TC0. Furthermore, if the class of GNNs are allowed to use random node initialization and global readout as in Abboud el al. (2020) then there is a matching lower bound in that they can compute exactly the same functions that can be expressed in TC0. This establishes an upper bound on the power of GNNs with random node features, by requiring the class of models to be of bounded depth (fixed #layers) and of size polynomial. While this result is still non-uniform, it improves the result of Abboud el al. (2020) where the construction can be worst-case exponential.
A fine-grained expressivity study of GNNs
Numerous recent works have analyzed the expressive power of MPNNs, primarily utilizing combinatorial techniques such as the 1-WL for the graph isomorphism problem. However, the graph isomorphism objective is inherently binary, not giving insights into the degree of similarity between two given graphs. Böker et al. (2023) resolve this issue by deriving continuous extensions of both 1-WL and MPNNs to graphons. Concretely, they show that the continuous variant of 1-WL delivers an accurate topological characterization of the expressive power of MPNNs on graphons, revealing which graphs these networks can distinguish and the difficulty level in separating them. They provide a theoretical framework for graph and graphon similarity, combining various topological variants of classical characterizations of the 1-WL. In particular, they characterize the expressive power of MPNNs in terms of the tree distance, which is a graph distance based on the concept of fractional isomorphisms, and substructure counts via tree homomorphisms, showing that these concepts have the same expressive power as the 1-WL and MPNNs on graphons. Interestingly, they also validated their theoretical findings by showing that randomly initialized MPNNs, without training, show competitive performance compared to their trained counterparts.
Expressiveness results for Subgraph GNNs
Subgraph-based GNNs were already a big trend in 2022 (Bevilacqua et al., 2022, Qian et al., 2022). This year, Zhang et al. (2023b) established more fine-grained expressivity results for such architectures. The paper investigates subgraph GNNs via the so-called Subgraph Weisfeiler-Leman Tests (SWL). Through this, they show a complete hierarchy of SWL with strictly growing expressivity. Concretely, they define equivalence classes for SWL-type algorithms and show that almost all existing subgraph GNNs fall in one of them. Moreover, the so-called SSWL achieves the maximal expressive power. Interestingly, they also relate SWL to several existing expressive GNNs architectures. For example, they show that SWL has the same expressivity as the local versions of 2-WL (Morris et al., 2020). In addition to theory, they also show that SWL-type architectures achieve good empirical results.
Expressive power of architectures for link prediction on KGs
The expressive power of architectures such as RGCN and CompGCN for link prediction on knowledge graphs has been studied by Barceló et al. (2022). This year, Huang et al. (2023) generalized these results to characterize the expressive power of various other model architectures.

Figure from Huang et al. (2023): The figure compares the respective mode of operations in R-MPNNs and C-MPNNs.
Huang et al. (2023) introduced the framework of conditional message passing networks (C-MPNNs) which includes architectures such as NBFNets. Classical relational message passing networks (R-MPNNs) are unary encoders (i.e., encoding graph nodes) and rely on a binary decoder for the task of link prediction (Zhang, 2021). On the other hand, C-MPNNs serve as binary encoders (i.e., encoding pairs of graph nodes) and as a result, are more suitable for the binary task of link prediction. C-MPNNs are shown to align with a relational Weisfeiler-Leman algorithm that can be seen as a local approximation of 2WL. These findings explain the superior performance of NBFNets and alike over, e.g., RGCNs. Huang et al. (2023) also present uniform expressiveness results in terms of precise logical characterizations for the class of binary functions captured by C-MPNNs.
Over-squashing and expressivity
Over-squashing is a phenomenon originally described by Alon & Yahav in 2021 as the compression of exponentially-growing receptive fields into fixed-size vectors. Subsequent research (Topping et al., 2022, Di Giovanni et al., 2023, Black et al., 2023, Nguyen et al., 2023) has characterised over-squashing through sensitivity analysis, proving that the dependence of the output features on hidden representations from earlier layers, is impaired by topological properties such as negative curvature or large commute time. Since the graph topology plays a crucial role in the formation of bottlenecks, graph rewiring, a paradigm shift elevating the graph connectivity to design factor in GNNs, has been proposed as a key strategy for alleviating over-squashing (if you are interested, see the Section on Exotic Message Passing below).

For the given graph, the MPNN learns stronger mixing (tight springs) for nodes (v, u) and (u, w) since their commute time is small, while nodes (u, q) and (u, z), with high commute-time, have weak mixing (loose springs). Source: Di Giovanni et al., 2023
Over-squashing is an obstruction to the expressive power, for it causes GNNs to falter in tasks with long-range interactions. To formally study this, Di Giovanni et al., 2023 introduce a new metric of expressivity, referred to as “mixing”, which encodes the joint and nonlinear dependence of a graph function on pairs of nodes’ features: for a GNN to approximate a function with large mixing, a necessary condition is allowing “strong” message exchange between the relevant nodes. Hence, they postulate to measure over-squashing through the mixing of a GNN prediction, and prove that the depth required by a GNN to induce enough mixing, as required by the task, grows with the commute time — typically much worse than the shortest-path distance. The results show how over-squashing hinders the expressivity of GNNs with “practical” size, and validate that it arises from the misalignment between the task (requiring strong mixing between nodes i and j) and the topology (inducing large commute time between i and j).
The “mixing” of a function pertains to the exchange of information between nodes, whatever this information is, and not to its capacity to separate node representations. In fact, these results also hold for GNNs more powerful than the 1-WL test. The analysis in Di Giovanni et al., (2023) offers an alternative approach for studying the expressivity of GNNs, which easily extends to equivariant GNNs in 3D space and their ability to model interactions between nodes.
Generalization and extrapolation capabilities of GNNs
The expressive power of MPNNs has achieved a lot of attention in recent years through its connection to the WL test. While this connection has led to significant advances in understanding and enhancing MPNNs’ expressive power (Morris et al, 2023a), it does not provide insights into their generalization performance, i.e., their ability to make meaningful predictions beyond the training set. Surprisingly, only a few notable contributions study MPNNs’ generalization behaviors, e.g., Garg et al. (2020), Kriege et al. (2018), Liao et al. (2021), Maskey et al. (2022), Scarselli et al. (2018). However, these approaches express MPNNs’ generalization ability using only classical graph parameters, e.g., maximum degree, number of vertices, or edges, which cannot fully capture the complex structure of real-world graphs. Further, most approaches study generalization in the non-uniform regime, i.e., assuming that the MPNNs operate on graphs of a pre-specified order.

Figure from Morris et al. (2023b): Overview of the generalization capabilities of MPNNs and their link to the 1-WL.
Hence, Morris et al. (2023b) showed a tight connection between the expressive power of the 1-WL and generalization performance. They investigate the influence of graph structure and the parameters’ encoding lengths on MPNNs’ generalization by tightly connecting 1-WL’s expressivity and MPNNs’ Vapnik–Chervonenkis (VC) dimension. To that, they show several results.
1️⃣ First, in the non-uniform regime, they show that MPNNs’ VC dimension depends tightly on the number of equivalence classes computed by the 1-WL over a set of graphs. In addition, their results easily extend to the k-WL and many recent expressive MPNN extensions.
2️⃣ In the uniform regime, i.e., when graphs can have arbitrary order, they show that MPNNs’ VC dimension is lower and upper bounded by the largest bitlength of its weights. In both the uniform and non-uniform regimes, MPNNs’ VC dimension depends logarithmically on the number of colors computed by the 1-WL and polynomially on the number of parameters. Moreover, they also empirically show that their theoretical findings hold in practice to some extent.
? Predictions time!
Christopher Morris (RWTH Aachen)
“I believe that there is a pressing need for a better and more practical theory of generalization of GNNs. ” — Christopher Morris (RWTH Aachen)
➡️ For example, we need to understand how graph structure and various architectural parameters influence generalization. Moreover, the dynamics of SGD for training GNNs are currently understudied and not well understood, and more works will study this.
İsmail İlkan Ceylan (Oxford)
“I hope to see more expressivity results in the uniform setting, where we fix the parameters of a neural network and examine its capabilities.” — İsmail İlkan Ceylan (Oxford)
➡️ In this case, we can identify a better connection to generalization, because if a property cannot be expressed uniformly then the model cannot generalise to larger graph sizes.
➡️ This year, we may also see expressiveness studies that target graph regression or graph generation, which remain under-explored. There are good reasons to hope for learning algorithms which are isomorphism-complete on larger graph classes, strictly generalizing the results for planar graphs.
➡️ It is also time to develop a theory for learning with fully relational data (i.e., knowledge hypergraphs), which will unlock applications in relational databases!
Francesco Di Giovanni (Oxford)
In terms of future theoretical developments of GNNs, I can see two directions that deserve attention.
“There is very little understanding of the dynamics of the weights of a GNN under gradient flow (or SGD); assessing the impact of the graph topology on the evolution of the weights is key to addressing questions about generalisation and hardness of a task.” — Francesco Di Giovanni (Oxford)
➡️ Second, I believe it would be valuable to develop alternative paradigms of expressivity, which more directly focus on approximation power (of graph functions and their derivatives) and identify precisely the tasks which are hard to learn. The latter direction could also be particularly meaningful for characterising the power of equivariant GNNs in 3D space, where measurements of expressivity might need to be decoupled from the 2D case in order to be better aligned with tasks coming from the scientific domain.
At the end: a fun fact about where WL went in 2023

Portraits: Ihor Gorsky
Predictions from the 2023 post
(1) More efforts on creating time- and memory-efficient subgraph GNNs.
❌ not really
(2) Better understanding of generalization of GNNs
✅ yes, see the subsections on oversquashing and generalization
(3) Weisfeiler and Leman visit 10 new places!
❌ (4 so far) Grammatical, indifferent, measurement modeling, paths
New and exotic message passing
Ben Finkelshtein (Oxford), Francesco Di Giovanni (Oxford), Petar Veličković (Google DeepMind)
Petar Veličković (Google DeepMind)
Over the years, it has become part of common folklore that the development of message passing operators has saturated. What I find particularly exciting about the progress made in 2023 is that, from several independent research groups (including our own), a unified novel direction has emerged: let’s start considering the impact of time in the GNN ⏳.
“I forecast that, in 2024, time will assume a central role in the development of novel GNN architectures.” — Petar Veličković (Google DeepMind)
? Time has already been leveraged in GNN design when it is explicitly provided in the input (in spatiotemporal or fully dynamic graphs). This year, it has started to feature in research of GNN operators on static graph inputs. Several works are dropping the assumption of a unified, synchronised clock ⏱️ which forces all messages in a layer to be sent and received at once.
1️⃣ The first such work, GwAC ?, only played with rudimentary randomised message scheduling, but provided proofs for why such processing might yield significant improvements in expressive power. Co-GNNs ? carry the torch further, demonstrating a more elaborate and fine-tuned message scheduling mechanism which is node-centric, allowing each node to choose when to send ? or receive ? messages. Co-GNNs also provide a practical method for training such schedulers by gradient descent. While the development of such asynchronous GNN models is highly desirable, we must also acknowledge the associated scalability issues — our present frontier hardware is not designed to efficiently scale such sequential systems.
2️⃣ In our own work on asynchronous algorithmic alignment, we instead opt to design a synchronous GNN, but constrain its message, aggregation, and update functions such that the GNN would yield identical embeddings even if parts of its dataflow were made asynchronous. This led us to an exciting journey through monoids, 1-cocycles, and category theory, resulting in a scalable GNN model that achieves superior performance on many CLRS-30 tasks.

A possible execution trace of an asynchronous GNN. While traditional GNNs send and receive all messages synchronously, under our framework, at any step the GNN may choose to execute any number of possible operations (depicted here with a collection on the right side of the graph). Source: Dudzik et al.
➡️ Lastly, it is worth noting that for certain special choices of message scheduling, we do not need to make modifications to synchronous GNNs’ architecture — and may instead resort to dynamic graph rewiring. DREW and Half-Hop are two concurrently published papers at ICML’23 which embody the principle of using graph rewiring to slow down message passing ?. In DREW, a message from each node is actually sent to every other node, but it takes k layers before a message will reach a neighbour that is k hops away! Half-Hop, on the other hand, takes a more lenient approach, and just randomly decides whether or not to introduce a “slow node” which extends the path between any two nodes connected by an edge. Both approaches naturally alleviate the oversmoothing problem, as messages travelling longer distances will oversmooth less.
Whether it is used for message passing design, GNN dataflow or graph rewiring, in 2023 we have just started to grasp the importance of time — even when time variation is not explicitly present in our dataset.
Ben Finkelshtein (Oxford)
The time-dependent message passing paradigm presented in Co-GNNs is a learnable generalisation of message passing, which allows each node to decide how to propagate information from or to its neighbours, thus enabling a more flexible flow of information. The nodes are regarded as players that can either broadcast to neighbors that listen and listen to neighbors that broadcast (like in classical message-passing), Broadcast to neighbors that listen, or Isolate (neither listen nor broadcast).
The interplay between these actions and the ability to change them locally and dynamically allows CoGNNs to determine a task-specific computational graph (which can be considered as a form of dynamic and directed rewiring, learn different action distribution for two nodes with different node features (both feature- and structure-based). CoGNNs allow asynchronous updates across nodes and also yield unique node identifiers with high probability, which allows them to distinguish any pair of graphs (more expressive than 1-WL, at the expense of equivariance holding only in expectation).

Left to right: classical MPNNs (all nodes broadcast & listen), DeepSets (all nodes isolate), and generic CoGNNs. Figure from blog post.
Check the Medium post for more details:
Co-operative Graph Neural Networks
Francesco Di Giovanni (Oxford)
“The understanding of over-squashing, arising when the task depends on the interaction between nodes with large commute time, acted as a catalyst for the emergence of graph rewiring as a valid approach for designing new GNNs.” — Francesco Di Giovanni (Oxford)
️? Graph rewiring broadly entails altering the connectivity of the input graph to facilitate the solution of the downstream task. Recently, this has often targeted bottlenecks in the graph, thereby adding (and removing) edges to improve the flow of information. While the emphasis has been on where messages are exchanged, recent works (discussed above) have shed light on the relevance of when messages should be exchanged as well. One rationale behind these approaches, albeit often implicit, is that the hidden representations built by the layers of a GNN, provide the graph with an (artificially) dynamic component, even though the graph and input features are static. This perspective can be leveraged in several ways.

In the classicical MPNN setting, at every layer information only travels from a node to its immediate neighbours. In DRew, the graph changes based on the layer, with newly added edges connecting nodes at distance r from layer r − 1 onward. Finally, in νDRew, we also introduce a delay mechanism equivalent to skip-connections between different nodes based on their mutual distance. Source: Gutteridge et al.
➡️ One framework that has particularly embraced such an angle is DRew, which extends any message-passing model in two ways: (i) it connects nodes at distance r directly, but only from layer r onwards; (ii) when nodes are connected, a delay is applied to their message exchange, based on their mutual distance. As the figure above illustrates, (i) allows the network to better retain the inductive bias, as nodes that are closer, interact earlier; (ii) instead acts as distance-aware skip connections, thereby facilitating the propagation of gradients for the loss. Most likely, it is for this reason, and not prevention of over-smoothing (which hardly has an impact for graph-level tasks), that the framework significantly enhances the performance of standard GNNs at larger depths (more details can be found in this blog post).
? Predictions: I believe that the deep implications of extending message-passing over the “time” component would start to emerge in the coming year. Works like DRew have only scratched the surface of why rewiring over time (beyond space) might benefit the training of GNNs, drastically affecting their accuracy response across different depth regimes.
➡️ More broadly, I hope that theoretical and practical developments of graph rewiring could be translated into scientific domains, where equivariant GNNs are often applied to 3D problems which either do not have a natural graph structure (making the question of “where” messages should be exchanged ever more relevant) or (and) exhibit natural temporal (multi-scale) properties (making the question of “when” messages should be exchanged likely to be key for reducing memory constraints and retaining the right inductive bias).
Geometry, Topology, Geometric Algebras & PDEs
Johannes Brandstetter (JKU Linz), Michael Galkin (Intel), Mathilde Papillon (UC Santa Barbara), Bastian Rieck (Helmholtz & TUM), and David Ruhe (U Amsterdam)
2023 brought the most comprehensive introduction to (and a survey of) Geometric GNNs covering the most basic and necessary concepts with a handful of examples: A Hitchhiker’s Guide to Geometric GNNs for 3D Atomic Systems (Duval, Mathis, Joshi, Schmidt, et al.). If you ever wanted to learn from scratch the core architectures powering recent breakthroughs of graph ML in protein design, material discovery, molecular simulations, and more — this is what you need!

Timeline of key Geometric GNNs for 3D atomic systems, characterised by the type of intermediate representations within layers. Source: Duval, Mathis, Joshi, Schmidt, et al.
Topology
? Working with topological structures in 2023 has become much easier for both researchers and practitioners thanks to the amazing efforts of the PyT team and their suite of resources: TopoNetX, TopoModelX, and TopoEmbedX. TopoNetX is pretty much the networkx for topological data. TopoNetX supports standard structures like cellular complexes, simplicial complexes, and combinatorial complexes. TopoModelX is a PyG-like library for deep learning on topological data and implements famous models like MPSN and CIN with a neat unified interface (the original PyG implementations are quite tangled). TopoEmbedX helps to train embedding models on topological data and supports core algorithms like Cell2Vec.

Domains: Nodes in blue, (hyper)edges in pink, and faces in dark red. Source: TopoNetX, Papillon et al
? A great headstart to the field and basic building blocks of those topological networks are the papers by Hajij et al and by Papillon et al. A notable chunk of models was implemented by the members of the Topology, Algebra, and Geometry in Data Science (TAG) community that regularly organizes topological workshops at ML conferences.
Mathilde Papillon (UCSB)
“Until 2023, the field of topological deep learning featured a fractured landscape of enriched representations for relational data.” — Mathilde Papillon (UC Santa Barbara)
➡️ Message-passing models were only built upon and benchmarked against other models of the same domain, e.g., the simplicial complex community remained insular to the hypergraph community. To make matters worse, most models adopted a unique mathematical notation. Deciding which model would be best suited to a given application seemed like a monumental task. A unification theory proposed by Hajij et al offered a general scheme under which all models could be systematically described and classified. We applied this theory to the literature to produce a comprehensive yet concise survey of message passing in topological deep learning that also serves as an accessible introduction to the field. We additionally provide a dictionary listing all the model architectures in one unifying notation.
➡️ To further unify the field, we organized the first Topological Deep Learning Challenge, hosted at the 2023 ICML TAG workshop and recorded via this white paper by Papillon et al. The goal was to foster reproducible research by crowdsourcing the open-source implementation of neural networks on topological domains. As part of the challenge, participants from around the world contributed implementations of pre-existing topological deep learning models in TopoModelX. Each submission was rigorously unit-tested and included benchmark training on datasets loaded from TopoNetX. It is our hope that this one-stop-shop suite of consistently implemented models will help practitioners test-drive topological methods for new applications and developments in 2024.
Bastian Rieck (Helmholtz & TUM)
2023 was an exciting year for topology-driven machine learning methods. On the one hand, we saw more integrations with geometrical concepts like curvature, thus demonstrating the versatility of hybrid geometrical-topological models. For instance, in ‘Curvature Filtrations for Graph Generative Model Evaluation,’ we showed how to employ curvature as a way to select suitable graph generative models. Here, curvature serves as a ‘lens’ that we use to extract graph structure information, while we employ persistent homology, a topological method, to compare this information in a consistent fashion.

An overview of the pipeline for evaluating graph generative models using discrete curvature. The ordering on edges gives rise to a curvature filtration, followed by a corresponding persistence diagram and landscape. For graph generative models, we select a curvature, apply this framework element-wise, and evaluate the similarity of the generated and reference distributions by comparing their average landscapes. Source: Southern, Wayland, Bronstein, and Rieck.
➡️ Another direction that serves to underscore that topology-driven methods are becoming a staple in graph learning research uses topology to assess the expressivity of graph neural network models. Sometimes, as in a very fascinating work from NeurIPS 2023 by Immonen et al. this even leads to novel models that leverage both geometrical and topological aspects of graphs in tandem! My own research also aims to contribute to this facet by specifically analyzing the expressivity of persistent homology in graph learning.
“2023 also was the cusp of moving away — or beyond — persistent homology. Despite being rightfully seen as the paradigmatic algorithm for topology-driven machine learning, algebraic topology and differential topology offer an even richer fabric that can be used to analyse data.” — Bastian Rieck (Helmholtz & TUM)
➡️ With my great collaborators, we started looking at some alternatives very recently and came up with the concept of neural differential forms. Differential forms permit us to elegantly build a bridge between geometry and topology by means of the de Rham cohomology — a way to link the integration of certain objects (differential forms), i.e. a fundamentally geometric operation, to topological characteristics of input data. With some additional constructions, the de Rham cohomology permits us to learn geometric descriptions of graphs (or higher-order combinatorial complexes) and solve learning tasks without having to rely on message passing. The upshot are models with fewer parameters that are potentially more effective at solving such tasks. There’s more to come here, since we have just started scratching the surface!
?My hopeful predictions for 2024 are that we will:
1️⃣ see many more diverse tools from algebraic and differential topology applied to graphs and combinatorial complexes,
2️⃣ better understand message passing on higher-order input data, and
3️⃣ finally obtain better parallel algorithms for persistent homology to truly unleash its power in a deep learning setting. A recent paper on spectral sequences by Torras-Casas reports some very exciting results that show the great prospects of this technique.
Geometric Algebras
Johannes Brandstetter (JKU Linz) and David Ruhe (U Amsterdam)
“In 2023, we saw the subfield of deep learning on geometric algebras (also known as Clifford algebras) take off. Previously, neural network layers formulated as operations on Clifford algebra multivectors were introduced by Brandstetter et al. This year, the ‘geometric’ in ‘geometric algebra’ was clearly put into action.” — Johannes Brandstetter (JKU Linz) and David Ruhe (U Amsterdam)
➡️ First, Ruhe et al. applied the quintessence of modern (plane-based) geometric algebra by introducing Geometric Clifford Algebra Networks (GCAN), neural network templates that model symmetry transformations described by various geometric algebras. We saw an intriguing application thereof by Pepe et al. in CGAPoseNet, building a geometry-aware pipeline for camera pose regression. Next, Ruhe et al. introduced Clifford Group Equivariant Neural Networks (CGENN), building steerable O

CGENNs (represented with ϕ) are able to operate on multivectors (elements of the Clifford algebra) in an O
➡️ Coincidently, Brehmer et al. formulated Geometric Algebra Transformer(GATr), a scalable Transformer architecture that harnesses the benefits of representations provided by the projective geometric algebra and the scalability of Transformers to build E(3)-equivariant architectures. The GATr architecture was extended to other algebras by Haan et al. who also examine which flavor of geometric algebra is best suited for your E(3)-equivariant machine learning problem.

Overview of the GATr architecture. Boxes with solid lines are learnable components, those with dashed lines are fixed. Source: Brehmer et al.
? In 2024, we can expect exciting new applications from these advancements. Some examples include the following.
1️⃣ We can expect explorations of their applicability to molecular data, drug design, neural physics emulations, crystals, etc. Other geometry-aware applications include 3D rendering, pose estimations, and planning for, e.g., robot arms.
2️⃣ We can expect the extension of geometric algebra-based networks to other neural network architectures, such as convolutional neural networks.
3️⃣ Next, the generality of the CGENN allows for explorations in other dimensions, e.g., 2D, but also in settings where data of various dimensionalities should be processed together. Further, they enable non-Euclidean geometries, which have several use cases in relativistic physics.
4️⃣ Finally, GATr and CGENN can be extended and applied to projective, conformal, hyperbolic, or elliptic geometries.
PDEs
Johannes Brandstetter (JKU Linz)
Concerning the landscape of neural PDE modelling, what topics have surfaced or gathered momentum through 2023?
1️⃣ To begin, there is a noticeable trend towards modelling PDEs on and within intricate geometries, necessitating a mesh-based discretization of space. This aligns with the overarching goal to address increasingly realistic real world problems. For example, Li et al. have introduced Geometry-Informed Neural Operator (GINO) for large-scale 3D PDEs.
2️⃣ Secondly, the development of neural network surrogates for Lagrangian-based simulations is becoming increasingly intriguing. The Lagrangian discretization of space uses finite material points which are tracked as fluid parcels through space and time. The most prominent Lagrangian discretization scheme is called smoothed particle hydrodynamics (SPH), which is the numerical baseline in the LagrangeBench benchmark dataset provided by Toshev et al.

Time snapshots of our datasets, at the initial time (top), 40% (middle), and 95% (bottom) of the trajectory. Color temperature represents velocity magnitude. (a) Taylor Green vortex (2D and 3D), (b) Reverse Poiseuille flow (2D and 3D), © Lid-driven cavity (2D and 3D), (d) Dam break (2D). Source: LagrangeBench by Toshev et al.
3️⃣ Thirdly, diffusion-based modelling is also not stopping for PDEs. We roughly see two directions. The first direction recasts the iterative nature of the diffusion process into a refinement of a candidate state initialised from noise and conditioned on previous timesteps. This iterative refinement was introduced in PDE-Refiner (Lippe et al.) and a variant thereof was already applied in GenCast (Price et al.). The second direction exerts the probabilistic nature of diffusion models to model chaotic phenomena such as 3D turbulence. Examples of this can be found in Turbulent Flow Simulation (Kohl et al.) and in From Zero To Turbulence (Lienen et al.). Especially for 3D turbulence, there are a lot of interesting things that will happen in the near future.
“Weather modelling has become a great success story over the last months. There is potentially much more exciting stuff to come, especially regarding weather forecasting directly from observational data or when building weather foundation models.” — Johannes Brandstetter (JKU Linz)
? What to expect in 2024:
1️⃣ More work regarding 3D turbulence modelling.
2️⃣ Multi-modality aspects of PDEs might emerge. This could include combining different PDEs, different resolutions, or different discretization schemes. We are already seeing a glimpse thereof in e.g. Multiple Physics Pretraining for Physical Surrogate Models by McCabe et al.
Predictions from the 2023 post
(1) Neural PDEs and their applications are likely to expand to more physics-related AI4Science subfields; computational fluid dynamics (CFD) will potentially be influenced by GNN.
✅ We are seeing 3D turbulence modelling, geometry-aware neural operators, particle-based neural surrogates, and a huge impact in e.g. weather forecasting.
(2) GNN based surrogates might augment/replace traditional well-tried techniques.
✅ Weather forecasting has become a great success story. Neural network based weather forecasts overtake traditional forecasts (medium range+local forecasts), e.g., GraphCast by Lam et al. and MetNet-3 by Andrychowicz et al.
Robustness and Explainability
Kexin Huang (Stanford)
“As GNNs are getting deployed in various domains, their reliability and robustness have become increasingly important, especially in safety-critical applications (e.g. scientific discovery) where the cost of errors is significant.” — Kexin Huang (Stanford)
1️⃣ When discussing the reliability of GNNs, a key criterion is uncertainty quantification — quantifying how much the model knows about the prediction. There are numerous works on estimating and calibrating uncertainty, also designed specifically for GNNs (e.g. GATS). However, they fall short of achieving pre-defined target coverage (i.e. % of points falling into the prediction set) both theoretically and empirically. I want to emphasize that this notion of having a coverage guarantee is critical especially in ML deployment for scientific discovery since practitioners often trust a model with statistical guarantees.
2️⃣ Conformal prediction is an exciting direction in statistics where it has finite sample coverage guarantees and has been applied in many domains such as vision and NLP. But it is unclear if it can be used in graphs theoretically since it is not obvious if the exchangeability assumption holds for graph settings. In 2023, we see conformal prediction has been extended to graphs. Notably, CF-GNN and DAPS have derived theoretical conditions for conformal validity in transductive node-level prediction setting and also developed methods to reduce the prediction set size for efficient downstream usage. More recently, we have also seen conformal prediction extensions to link prediction, non-uniform split, edge exchangeability, and also adaptations for settings where exchangeability does not hold (such as inductive setting).

Conformal prediction for graph-structured data. (1) A base GNN model (GNN) that produces prediction scores µ for node i. (2) Conformal correction. Since the training step is not aware of the conformal calibration step, the size/length of prediction sets/intervals (i.e. efficiency) are not optimized. We use a topology-aware correction model that takes µ as the input node feature and aggregates information from its local subgraph to produce an updated prediction µ˜. (3) Conformal prediction. We prove that in a transductive random split setting, graph exchangeability holds given permutation invariance. Thus, standard CP can be used to produce a prediction set/interval based on µ˜ that includes true label with pre-specified coverage rate 1-α. Source: Huang et al.
? Looking ahead, we expect more extensions to cover a wide range of GNN deployment use cases. Overall, I think having statistical guarantees for GNNs is very nice because it enables the trust of practitioners to use GNN predictions.
Graph Transformers
Chen Lin (Oxford)
? In 2023, we have seen the continuation of the rise of Graph Transformers. It has become the common GNN design, e.g., in GATr, the authors attribute its popularity to its “favorable scaling properties, expressiveness, trainability, and versatility”.
1️⃣ Expressiveness of GTs. As mentioned in the GNN Theory section, recent work from Cai et al. (2023) shows the equivalence between MPNNs with a Virtural Node and GTs under a non-uniform setting. This poses a question on how powerful are GTs and what is the source of their representation ability. Zhang et al. (2023) successfully combine a new powerful positional embedding (PE) to improve the expressiveness of their GTs, achieving expressivity over the biconnectivity problem. This gives evidence of the importance of PEs to the expressiveness of GTs. A recent submission GPNN provides a clearer view on the central role of the positional encoding. It has been shown that one can generalize the proof in Zhang et al. (2023) to show how GTs’ expressiveness is decided by various positional encodings.
2️⃣ Positional (Structural) Encoding. Given the importance of PE/SE to GTs, now we turn to the design of those expressive features usually derived from existing graph invariants. In 2022, GraphGPS observed a huge empirical success by combining GTs with various (or even multiple) PE/SEs. In 2023, more powerful PE/SE is available.
Relative Random Walk PE (RRWP) proposed by Ma et al generalizes the random walk structural encoding with the relational part. Together with a new variant of attention mechanism, GRIT achieves a strong empirical performance compared with existing PE/SEs on property prediction benchmarks (SOTA on ZINC). Theoretically, RRWP can approximate the Shortest path distance, personalized PageRank, and heat kernel with a specific choice of parameters. With RRWP, GRIT is more expressive than SPD-WL.

RRWP visualization for the fluorescein molecule, up to the 4th power. Thicker and darker edges indicate higher edge weight. Probabilities for longer random walks reveal higher-order structures (e.g., the cliques evident in 3-RW and the star patterns in 4-RW). Source: Ma et al.
Puny et al proposed a new theoretical framework for expressivity based on Equivariant Polynomials where the expressivity of common GNNs can be improved by having the polynomial features, computed with tensor contractions based on the equivariant basis, as positional encodings. The empirical results are surprising: GatedGCNs is improved from a test MAE of 0.265 to 0.106 with the d-expressive polynomials. It will be very interesting to see if someone combines this with GTs in the future.
3️⃣ Efficient GTs. It remains challenging for GTs to be applied to large graphs due to the O(N²) complexity. In 2023, we saw more works trying to eliminate such difficulty by lowering the computation complexity of GTs. Deac et al used expander graphs for the propagation, which is regularly connected with few edges. Exphormer extended this idea to GT by combining expander graphs with the local neighborhood aggregation and virtual node. Exphormer allows graph transformers to scale to larger graphs (as large as ogbn-arxiv with 169K nodes). It also achieved strong empirical results and ranked top on several Long-Range Graph Benchmark tasks.
? Moving forward to 2024:
- A better understanding of self-attention’s benefits on abstract beyond expressiveness.
- Big open-source pre-trained equivariant GT in 2024!
- More powerful positional encodings.
Structural biology: Pinder from VantAI, PoseBusters from Oxford, PoseCheck from The Other Place, DockGen, and LargeMix and UltraLarge datasets from Valence Labs
Temporal Graph Benchmark (TGB): Until now, progress in temporal graph learning has been held back by the lack of large high-quality datasets, as well as the lack of proper evaluation thus leading to over-optimistic performance. TGB addresses this by introducing a collection of seven realistic, large-scale and diverse benchmarks for learning on temporal graphs, including both node-wise and link-wise tasks. Inspired by the success of OGB, TGB automates dataset downloading and processing as well as evaluation protocols, and allows users to compare model performance using a leaderboard. Check out the associated blog post for more details.
TpuGraphs from Google Research: the graph property prediction dataset of TPU computational graphs. The dataset provides 25x more graphs than the largest graph property prediction dataset (with comparable graph sizes), and 770x larger graphs on average compared to existing performance prediction datasets on machine learning programs. Google ran Kaggle competition based off TpuGraphs!
LagrangeBench: A Lagrangian Fluid Mechanics Benchmarking Suite — where you can evaluate your favorite GNN-based simulator in a JAX-based environment (for JAX aficionados).
RelBench: Relational Deep Learning Benchmark from Stanford and Kumo.AI: make time-based predictions over relational databases (which you can model as graphs or hypergraphs).
The GNoMe dataset from Google DeepMind: 381k more novel stable materials for your materials discovery and ML potentials models!
Conferences, Courses & Community
The main events in the graph and geometric learning world (apart from big ML conferences) grow larger and more mature: The Learning on Graphs Conference (LoG), Molecular ML (MoML), and the Stanford Graph Learning Workshop. The LoG conference features a cool format with the remote-first conference and dozens of local meetups organized by community members spanning the whole globe from China to UK & Europe to the US West Coast ??? .

The LoG meetups in Amsterdam, Paris, Tromsø, and Shanghai. Source: Slack of the LoG community
Courses, books, and educational resources
- Geometric GNN Dojo — a pedagogical resource for beginners and experts to explore the design space of GNNs for geometric graphs (pairs best with the recent Hitchhiker’s Guide to Geometric GNNs).
- TorchCFM — the main entrypoint to the world of flow matching.
- The PyT team maintains TopoNetX, TopoModelX, and TopoEmbedX — the most hands-on libraries to jump into topological deep learning.
- The book on Equivariant and Coordinate Independent Convolutional Networks: A Gauge Field Theory of Neural Networks by Maurice Weiler, Patrick Forré, Erik Verlinde, and Max Welling — brings together the findings on the representation theory and differential geometry of equivariant CNNs
- ML for Science in Quantum, Atomistic, and Continuum systems by well over 60 authors from 23 institutions (Zhang, Wang, Helwig, Luo, Fu, Xie et al.)
- Scientific discovery in the age of artificial intelligence by Wang et al published in Nature.
- Learning on Graphs & Geometry
- Molecular Modeling and Drug Discovery (M2D2)
- VantAI reading group
- Oxford LoG2 seminar series
Memes of 2023

Commemorating the successes of flow matching in 2023 in the meme and unique t-shirts brought to NeurIPS’23. Right: Hannes Stärk and Michael Galkin are making a statement at NeurIPS’23. Images by Michael Galkin

GNN aggregation functions are actually portals to category theory (Created by Petar Veličković)

Michael Bronstein continues to harass Google by demanding his DeepMind chair at every ML conference, but so far, he has only been offered stools (photo credits: Jelani Nelson and Thomas Kipf).

The authors of this blog post congratulate you upon completing the long read. Michael Galkin and Michael Bronstein with the Meme of 2022 at ICML 2023 in Hawaii (Photo credit: Ben Finkelshtein)
For additional articles about geometric and graph deep learning, see Michael Galkin’s and Michael Bronstein’s Medium posts and follow the two Michaels (Galkin and Bronstein) on Twitter.
Graph & Geometric ML in 2024: Where We Are and What’s Next (Part I — Theory & Architectures) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
