Running large AI models on edge devices
Image created using Pixlr
AI models, particularly Large Language Models (LLMs), need large amounts of GPU memory. For example, in the case of the LLaMA 3.1 model, released in July 2024, the memory requirements are:
In a full-sized machine learning model, the weights are represented as 32-bit floating point numbers. Modern models have hundreds of millions to tens (or even hundreds) of billions of weights. Training and running such large models is very resource-intensive:
Being highly resource-intensive has two main drawbacks:
Thus, end-users and personal devices must necessarily access AI models via a paid API service. This leads to a suboptimal user experience for both consumer apps and their developers:
Reducing the size of AI models is therefore an active area of research and development. This is the first of a series of articles discussing ways of reducing model size, in particular by a method called quantization. These articles are based on studying the original research papers. Throughout the series, you will find links to the PDFs of the reference papers.
Not relying on expensive hardware would make AI applications more accessible and accelerate the development and adoption of new models. Various methods have been proposed and attempted to tackle this challenge of building high-performing yet small-sized models.
Low-rank decomposition
Neural networks express their weights in the form of high-dimensional tensors. It is mathematically possible to decompose a high-ranked tensor into a set of smaller-dimensional tensors. This makes the computations more efficient. This is known as Tensor rank decomposition. For example, in Computer Vision models, weights are typically 4D tensors.
Lebedev et al, in their 2014 paper titled Speeding-Up Convolutional Neural Networks Using Fine-Tuned Cp-Decomposition demonstrate that using a common decomposition technique, Canonical Polyadic Decomposition (CP Decomposition), convolutions with 4D weight tensors (which are common in computer vision models) can be reduced to a series of four convolutions with smaller 2D tensors. Low Rank Adaptation (LoRA) is a modern (proposed in 2021) technique based on a similar approach applied to Large Language Models.
Pruning
Another way to reduce network size and complexity is by eliminating connections from a network. In a 1989 paper titled Optimal Brain Damage, Le Cun et al propose deleting connections with small magnitudes and retraining the model. Applied iteratively, this approach reduces half or more of the weights of a neural network. The full paper is available on the website of Le Cun, who (as of 2024) is the chief AI scientist at Meta (Facebook).
In the context of large language models, pruning is especially challenging. SparseGPT, first shared by Frantar et al in a 2023 paper titled SparseGPT: Massive Language Models Can be Accurately Pruned in One-Shot, is a well-known pruning method that successfully reduces by half the size of LLMs without losing much accuracy. Pruning LLMs to a fraction of their original size has not yet been feasible. The article, Pruning for Neural Networks, by Lei Mao, gives an introduction to this technique.
Knowledge Distillation
Knowledge transfer is a way of training a smaller (student) neural network to replicate the behavior of a larger and more complex (teacher) neural network. In many cases, the student is trained based on the final prediction layer of the teacher network. In other approaches, the student is also trained based on the intermediate hidden layers of the teacher. Knowledge Distillation has been used successfully in some cases, but in general, the student networks are unable to generalize to new unseen data. They tend to be overfitted to replicate the teacher’s behavior within the training dataset.
Quantization
In a nutshell, quantization involves starting with a model with 32-bit or 16-bit floating point weights and applying various techniques to reduce the precision of the weights, to 8-bit integers or even binary (1-bit), without sacrificing model accuracy. Lower precision weights have lower memory and computational needs.
The rest of this article, from the next section onwards, and the rest of this series give an in-depth understanding of quantization.
Hybrid
It is also possible to apply different compression techniques in sequence. Han et al, in their 2016 paper titled Compressing Deep Neural Networks with Pruning, Trained Quantization, and Huffman Coding, apply pruning followed by quantization followed by Huffman coding to compress the AlexNet model by a factor of 35X, to reduce the model size from 240 MB to 6.9 MB without significant loss of accuracy. As of July 2024, such approaches have yet to be tried on low-bit LLMs.
Quantization 101
The “size” of a model is mainly determined by two factors:
It is well-established that the number of parameters in a model is crucial to its performance — hence, reducing the number of parameters is not a viable approach. Thus, attempting to reduce the length of each weight is a more promising angle to explore.
Traditionally, LLMs are trained with 32-bit weights. Models with 32-bit weights are often referred to as full-sized models. Reducing the length (or precision) of model parameters is called quantization. 16-bit and 8-bit quantization are common approaches. More radical approaches involve quantizing to 4 bits, 2 bits, and even 1 bit. To understand how higher precision numbers are quantized to lower precision numbers, refer to Quantizing the Weights of AI Models, with examples of quantizing model weights.
Quantization helps with reducing the memory requirements and reducing the computational cost of running the model. Typically, model weights are quantized. It is also common to quantize the activations (in addition to quantizing the weights). The function that maps the floating point weights to their lower precision integer versions is called the quantizer, or quantization function.
Quantization in Neural Networks
Simplistically, the linear and non-linear transformation applied by a neural network layer can be expressed as:
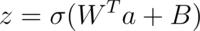
In the above expression:
Most of the computational workload in running neural networks comes from the convolution operation — which involves the multiplication of many floating point numbers. Large models with many weights have a very large number of convolution operations.
This computational cost could potentially be reduced by doing the multiplication in lower-precision integers instead of floating-point numbers. In an extreme case, as discussed in Understanding 1.58-bit Language Models, the 32-bit weights could potentially be represented by ternary numbers {-1, 0, +1} and the multiplication operations would be replaced by much simpler addition and subtraction operations. This is the intuition behind quantization.
The computational cost of digital arithmetic is quadratically related to the number of bits. As studied by Siddegowda et al in their paper on Neural Network Quantization (Section 2.1), using 8-bit integers instead of 32-bit floats leads to 16x higher performance, in terms of energy consumption. When there are billions of weights, the cost savings are very significant.
The quantizer function maps the high-precision (typically 32-bit floating point weights) to lower-precision integer weights.
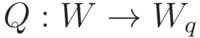
The “knowledge” the model has acquired via training is represented by the value of its weights. When these weights are quantized to lower precision, a portion of their information is also lost. The challenge of quantization is to reduce the precision of the weights while maintaining the accuracy of the model.
One of the main reasons some quantization techniques are effective is that the relative values of the weights and the statistical properties of the weights are more important than their actual values. This is especially true for large models with millions or billions of weights. Later articles on quantized BERT models — BinaryBERT and BiBERT, on BitNet — which is a transformer LLM quantized down to binary weights, and on BitNet b1.58 — which quantizes transformers to use ternary weights, illustrate the use of successful quantization techniques. A Visual Guide to Quantization, by Maarten Grootendoorst, has many illustrations and graphic depictions of quantization.
Quantized Inference
Inference means using an AI model to generate predictions, such as the classification of an image, or the completion of a text string. When using a full-precision model, the entire data flow through the model is in 32-bit floating point numbers. When running inference through a quantized model, many parts — but not all, of the data flow are in lower precision.
The bias is typically not quantized because the number of bias terms is much less than the number of weights in a model. So, the cost savings is not enough to justify the overhead of quantization. The accumulator’s output is in high precision. The output of the activation is also in higher precision.
Conclusion
This article discussed the need to reduce the size of AI models and gave a high-level overview of ways to achieve reduced model sizes. It then introduced the basics of quantization, a method that is currently the most successful in reducing model sizes while managing to maintain an acceptable level of accuracy.
The goal of this series is to give you enough background to appreciate the extreme quantization of language models, starting from simpler models like BERT before finally discussing 1-bit LLMs and the recent work on 1.58-bit LLMs. To this end, the next few articles in this series present a semi-technical deep dive into the different subtopics like the mathematical operations behind quantization and the process of training quantized models. It is important to understand that because this is an active area of research and development, there are few standard procedures and different workers adopt innovative methods to achieve better results.

Reducing the Size of AI Models was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

Image created using Pixlr
AI models, particularly Large Language Models (LLMs), need large amounts of GPU memory. For example, in the case of the LLaMA 3.1 model, released in July 2024, the memory requirements are:
- The 8 billion parameter model needs 16 GB memory in 16-bit floating point weights
- The larger 405 billion parameter model needs 810 GB using 16-bit floats
In a full-sized machine learning model, the weights are represented as 32-bit floating point numbers. Modern models have hundreds of millions to tens (or even hundreds) of billions of weights. Training and running such large models is very resource-intensive:
- It takes lots of compute (processing power).
- It requires large amounts of GPU memory.
- It consumes large amounts of energy, In particular, the biggest contributors to this energy consumption are:
- Performing a large number of computations (matrix multiplications) using 32-bit floats
- Data transfer — copying the model data from memory to the processing units.
Being highly resource-intensive has two main drawbacks:
- Training: Models with large GPU requirements are expensive and slow to train. This limits new research and development to groups with big budgets.
- Inference: Large models need specialized (and expensive) hardware (dedicated GPU servers) to run. They cannot be run on consumer devices like regular laptops and mobile phones.
Thus, end-users and personal devices must necessarily access AI models via a paid API service. This leads to a suboptimal user experience for both consumer apps and their developers:
- It introduces latency due to network access and server load.
- It also introduces budget constraints on developers building AI-based software. Being able to run AI models locally — on consumer devices, would mitigate these problems.
Reducing the size of AI models is therefore an active area of research and development. This is the first of a series of articles discussing ways of reducing model size, in particular by a method called quantization. These articles are based on studying the original research papers. Throughout the series, you will find links to the PDFs of the reference papers.
- The current introductory article gives an overview of different approaches to reducing model size. It introduces quantization as the most promising method and as a subject of current research.
- Quantizing the Weights of AI Models illustrates the arithmetics of quantization using numerical examples.
- Quantizing Neural Network Models discusses the architecture and process of applying quantization to neural network models, including the basic mathematical principles. In particular, it focuses on how to train models to perform well during inference with quantized weights.
- Different Approaches to Quantization explains different types of quantization, such as quantizing to different precisions, the granularity of quantization, deterministic and stochastic quantization, and different quantization methods used during training models.
- Extreme Quantization: 1-bit AI Models is about binary quantization, which involves reducing the model weights from 32-bit floats to binary numbers. It shows the mathematical principles of binary quantization and summarizes the approach adopted by the first researchers who implemented binary quantization of transformer-based models (BERT).
- Understanding 1-bit Large Language Models presents recent work on quantizing large language models (LLMs) to use 1-bit (binary) weights, i.e. {-1, 1}. In particular, the focus is on BitNet, which was the first successful attempt to redesign the transformer architecture to use 1-bit weights.
- Understanding 1.58-bit Language Models discusses the quantization of neural network models, in particular LLMs, to use ternary weights ({-1, 0, +1}). This is also referred to as 1.58-bit quantization and it has proved to deliver very promising results. This topic has attracted much attention in the tech press in the first half of 2024. The background explained in the previous articles helps to get a deeper understanding of how and why LLMs are quantized to 1.58 bits.
Not relying on expensive hardware would make AI applications more accessible and accelerate the development and adoption of new models. Various methods have been proposed and attempted to tackle this challenge of building high-performing yet small-sized models.
Low-rank decomposition
Neural networks express their weights in the form of high-dimensional tensors. It is mathematically possible to decompose a high-ranked tensor into a set of smaller-dimensional tensors. This makes the computations more efficient. This is known as Tensor rank decomposition. For example, in Computer Vision models, weights are typically 4D tensors.
Lebedev et al, in their 2014 paper titled Speeding-Up Convolutional Neural Networks Using Fine-Tuned Cp-Decomposition demonstrate that using a common decomposition technique, Canonical Polyadic Decomposition (CP Decomposition), convolutions with 4D weight tensors (which are common in computer vision models) can be reduced to a series of four convolutions with smaller 2D tensors. Low Rank Adaptation (LoRA) is a modern (proposed in 2021) technique based on a similar approach applied to Large Language Models.
Pruning
Another way to reduce network size and complexity is by eliminating connections from a network. In a 1989 paper titled Optimal Brain Damage, Le Cun et al propose deleting connections with small magnitudes and retraining the model. Applied iteratively, this approach reduces half or more of the weights of a neural network. The full paper is available on the website of Le Cun, who (as of 2024) is the chief AI scientist at Meta (Facebook).
In the context of large language models, pruning is especially challenging. SparseGPT, first shared by Frantar et al in a 2023 paper titled SparseGPT: Massive Language Models Can be Accurately Pruned in One-Shot, is a well-known pruning method that successfully reduces by half the size of LLMs without losing much accuracy. Pruning LLMs to a fraction of their original size has not yet been feasible. The article, Pruning for Neural Networks, by Lei Mao, gives an introduction to this technique.
Knowledge Distillation
Knowledge transfer is a way of training a smaller (student) neural network to replicate the behavior of a larger and more complex (teacher) neural network. In many cases, the student is trained based on the final prediction layer of the teacher network. In other approaches, the student is also trained based on the intermediate hidden layers of the teacher. Knowledge Distillation has been used successfully in some cases, but in general, the student networks are unable to generalize to new unseen data. They tend to be overfitted to replicate the teacher’s behavior within the training dataset.
Quantization
In a nutshell, quantization involves starting with a model with 32-bit or 16-bit floating point weights and applying various techniques to reduce the precision of the weights, to 8-bit integers or even binary (1-bit), without sacrificing model accuracy. Lower precision weights have lower memory and computational needs.
The rest of this article, from the next section onwards, and the rest of this series give an in-depth understanding of quantization.
Hybrid
It is also possible to apply different compression techniques in sequence. Han et al, in their 2016 paper titled Compressing Deep Neural Networks with Pruning, Trained Quantization, and Huffman Coding, apply pruning followed by quantization followed by Huffman coding to compress the AlexNet model by a factor of 35X, to reduce the model size from 240 MB to 6.9 MB without significant loss of accuracy. As of July 2024, such approaches have yet to be tried on low-bit LLMs.
Quantization 101
The “size” of a model is mainly determined by two factors:
- The number of weights (or parameters)
- The size (length in bits) of each parameter.
It is well-established that the number of parameters in a model is crucial to its performance — hence, reducing the number of parameters is not a viable approach. Thus, attempting to reduce the length of each weight is a more promising angle to explore.
Traditionally, LLMs are trained with 32-bit weights. Models with 32-bit weights are often referred to as full-sized models. Reducing the length (or precision) of model parameters is called quantization. 16-bit and 8-bit quantization are common approaches. More radical approaches involve quantizing to 4 bits, 2 bits, and even 1 bit. To understand how higher precision numbers are quantized to lower precision numbers, refer to Quantizing the Weights of AI Models, with examples of quantizing model weights.
Quantization helps with reducing the memory requirements and reducing the computational cost of running the model. Typically, model weights are quantized. It is also common to quantize the activations (in addition to quantizing the weights). The function that maps the floating point weights to their lower precision integer versions is called the quantizer, or quantization function.
Quantization in Neural Networks
Simplistically, the linear and non-linear transformation applied by a neural network layer can be expressed as:
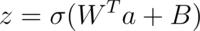
In the above expression:
- z denotes the output of the non-linear function. It is also referred to as the activation.
- Sigma is the non-linear activation function. It is often the sigmoid function or the tanh function.
- W is the weight matrix of that layer
- a is the input vector
- B is the bias vector
- The matrix multiplication of the weight and the input is referred to as convolution. Adding the bias to the product matrix is called accumulation.
- The term passed to the sigma (activation) function is called a Multiply-Accumulate (MAC) operation.
Most of the computational workload in running neural networks comes from the convolution operation — which involves the multiplication of many floating point numbers. Large models with many weights have a very large number of convolution operations.
This computational cost could potentially be reduced by doing the multiplication in lower-precision integers instead of floating-point numbers. In an extreme case, as discussed in Understanding 1.58-bit Language Models, the 32-bit weights could potentially be represented by ternary numbers {-1, 0, +1} and the multiplication operations would be replaced by much simpler addition and subtraction operations. This is the intuition behind quantization.
The computational cost of digital arithmetic is quadratically related to the number of bits. As studied by Siddegowda et al in their paper on Neural Network Quantization (Section 2.1), using 8-bit integers instead of 32-bit floats leads to 16x higher performance, in terms of energy consumption. When there are billions of weights, the cost savings are very significant.
The quantizer function maps the high-precision (typically 32-bit floating point weights) to lower-precision integer weights.
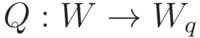
The “knowledge” the model has acquired via training is represented by the value of its weights. When these weights are quantized to lower precision, a portion of their information is also lost. The challenge of quantization is to reduce the precision of the weights while maintaining the accuracy of the model.
One of the main reasons some quantization techniques are effective is that the relative values of the weights and the statistical properties of the weights are more important than their actual values. This is especially true for large models with millions or billions of weights. Later articles on quantized BERT models — BinaryBERT and BiBERT, on BitNet — which is a transformer LLM quantized down to binary weights, and on BitNet b1.58 — which quantizes transformers to use ternary weights, illustrate the use of successful quantization techniques. A Visual Guide to Quantization, by Maarten Grootendoorst, has many illustrations and graphic depictions of quantization.
Quantized Inference
Inference means using an AI model to generate predictions, such as the classification of an image, or the completion of a text string. When using a full-precision model, the entire data flow through the model is in 32-bit floating point numbers. When running inference through a quantized model, many parts — but not all, of the data flow are in lower precision.
The bias is typically not quantized because the number of bias terms is much less than the number of weights in a model. So, the cost savings is not enough to justify the overhead of quantization. The accumulator’s output is in high precision. The output of the activation is also in higher precision.
Conclusion
This article discussed the need to reduce the size of AI models and gave a high-level overview of ways to achieve reduced model sizes. It then introduced the basics of quantization, a method that is currently the most successful in reducing model sizes while managing to maintain an acceptable level of accuracy.
The goal of this series is to give you enough background to appreciate the extreme quantization of language models, starting from simpler models like BERT before finally discussing 1-bit LLMs and the recent work on 1.58-bit LLMs. To this end, the next few articles in this series present a semi-technical deep dive into the different subtopics like the mathematical operations behind quantization and the process of training quantized models. It is important to understand that because this is an active area of research and development, there are few standard procedures and different workers adopt innovative methods to achieve better results.
Reducing the Size of AI Models was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
