- Регистрация
- 27 Февраль 2018
- Сообщения
- 12 302
- Лучшие ответы
- 0
- Баллы
- 1 293
Offline
Одна из экзотических форм материи — это квазикристаллы. Они сохраняют упорядоченную структуру, но она неидеальная и не является своей точной копией. Перспективным направлением для применения квазикристаллов считаются абсорбирующие вещества и синтез (сворачиваемость) белков. Команда физиков из Великобритании и Швейцарии взялась кардинально решить вопрос с проектированием таких структур, которые представляют собой также самые сложные в мире лабиринты.

Модель квазикристалла с гамильтоновым путём. Источник изображения: University of Bristol
Этой задаче, очевидно, намного больше лет, чем нам известно. По крайней мере, частный случай квазикристаллов был поднят учёными около 300 лет назад в задаче о ходе коня. Эта шахматная фигура должна была посетить каждое поле доски без повтора и вернуться в исходное положение. В общем случае подобное поведение называется гамильтоновым циклом (или путём, если не нужно возвращаться в точку старта). Если смотреть на проблему ещё шире, то речь идёт о создании фракталов — геометрических узоров на основе повторяющихся мелких элементов, подобных общей структуре.
В своём исследовании учёные использовали непериодическую мозаику (плитку) Амманна-Бенкера. Не менее известна мозаика Пенроуза. Этому графическому феномену уделил место и время современный американский писатель-фантаст Нил Стивенсон, используя его в произведении «Анафем», которое просто обязан прочесть каждый, кто интересуется естествознанием. Учёные использовали идею для моделирования циклов, в ходе которых каждый атом в кристаллической решётке квазикристалла мог быть посещён только один раз, что соединяет все атомы от начала до конца в одну и никогда не пересекающуюся линию. Более того, подобную структуру можно бесконечно масштабировать подобно фракталам.
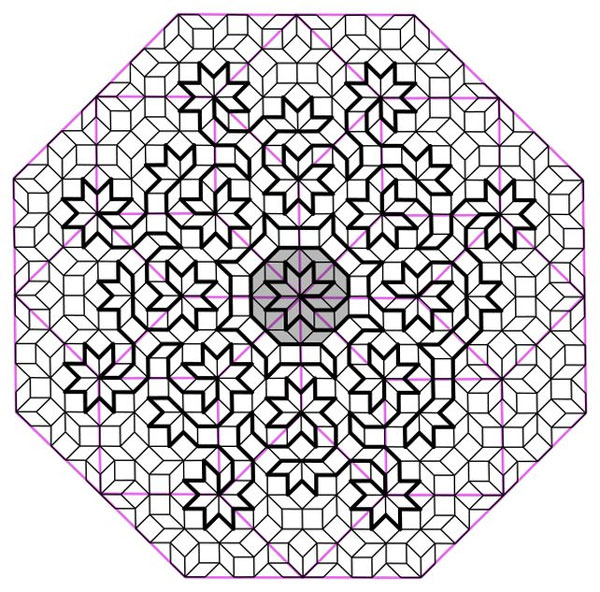
Мозаика (плитка) Амманна-Бенкера
Целью проделанной работы не было создание головоломок-лабиринтов для развлечения скучающих граждан. Во-первых, новая модель может помочь с оптимизацией логистических задач. Также с её помощью может решаться проблема получения новых пространственных форм (сворачивания) белков. Наконец, поглощение углекислого газа или других молекул будет намного эффективнее, если использовать подобные лабиринтообразные кристаллические структуры. Фрактальность в таком случае умножит эффект за счёт потенциальной возможности дробления на более мелкие части.

Модель квазикристалла с гамильтоновым путём. Источник изображения: University of Bristol
Этой задаче, очевидно, намного больше лет, чем нам известно. По крайней мере, частный случай квазикристаллов был поднят учёными около 300 лет назад в задаче о ходе коня. Эта шахматная фигура должна была посетить каждое поле доски без повтора и вернуться в исходное положение. В общем случае подобное поведение называется гамильтоновым циклом (или путём, если не нужно возвращаться в точку старта). Если смотреть на проблему ещё шире, то речь идёт о создании фракталов — геометрических узоров на основе повторяющихся мелких элементов, подобных общей структуре.
В своём исследовании учёные использовали непериодическую мозаику (плитку) Амманна-Бенкера. Не менее известна мозаика Пенроуза. Этому графическому феномену уделил место и время современный американский писатель-фантаст Нил Стивенсон, используя его в произведении «Анафем», которое просто обязан прочесть каждый, кто интересуется естествознанием. Учёные использовали идею для моделирования циклов, в ходе которых каждый атом в кристаллической решётке квазикристалла мог быть посещён только один раз, что соединяет все атомы от начала до конца в одну и никогда не пересекающуюся линию. Более того, подобную структуру можно бесконечно масштабировать подобно фракталам.

Мозаика (плитка) Амманна-Бенкера
Целью проделанной работы не было создание головоломок-лабиринтов для развлечения скучающих граждан. Во-первых, новая модель может помочь с оптимизацией логистических задач. Также с её помощью может решаться проблема получения новых пространственных форм (сворачивания) белков. Наконец, поглощение углекислого газа или других молекул будет намного эффективнее, если использовать подобные лабиринтообразные кристаллические структуры. Фрактальность в таком случае умножит эффект за счёт потенциальной возможности дробления на более мелкие части.
